Uma partícula de massa se move ao longo de um eixo sob a ação de uma única força que é conservativa. A energia potencial associada a essa força está representada no gráfico ao lado. No ponto , a velocidade da partícula é .
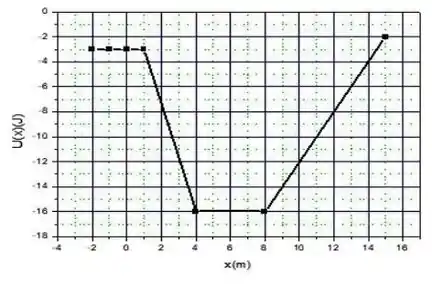
(a) Encontre o módulo e o sentido de em .
(b) Obtenha a energia mecânica dessa partícula.
(c) Determine a energia potencial no ponto. NOTA: .
Passo 1
Na letra (a), queremos a força no momento em que a partícula passa por .
Temos um gráfico da energia potencial para retirar essa informação...
Mas que que eu vou fazer com esse gráfico?

Então... pensa na energia mecânica.
Como a única força que atua na partícula é , uma força conservativa, a energia mecânica do sistema se conserva.
Okay, e daí?
Se a energia mecânica do sistema se conserva (constante), isso significa que a energia transita entre a forma de energia cinética e energia potencial .
Como uma força atuando sobre a partícula faz ela ganhar ou perder velocidade, ela vai ganhar ou perder energia cinética .
Para que a energia mecânica não se altere, quando mudar, a energia potencial vai ter que compensar essa mudança, para isso ela vai variar exatamente o oposto da energia cinética .
Quanto maior a força , mais rapidamente vai variar, e, consequentemente, mais rapidamente vai variar também. Podemos usar aquela relação que diz que a menos a variação de (sua derivada) é igual à força:
Passo 2
Como a derivada de um gráfico nos dá a inclinação dele, vamos calcular a inclinação daquele trecho da reta que inclui o .
Para achar a inclinação de uma reta, basta a gente pegar dois pontos e calcular a variação de sobre a variação de :
Vamos pegar no gráfico dois pontos, por exemplo esses aqui:
Então:
Passo 3
Então, conseguimos o módulo da força :
Passo 4
E o sentido da força?
Como achamos positiva, ela aponta no sentido positivo de .
Isso faz sentido, pois se a partícula estiver caminhando no sentido positivo do eixo , para sua energia diminuir, sua energia deve aumentar. Se a energia cinética aumenta, sua velocidade aumenta, logo, a força está a favor do movimento (sentido positivo de ).
Então temos que:
e aponta para o sentido positivo de .
Passo 5
Na letra (b), queremos a energia mecânica da partícula.
Como a energia mecânica é a mesma em todo o trajeto (se conserva), podemos usar qualquer ponto para calcularmos isso.
O enunciado nos deu a velocidade da partícula em :
Assim, conseguimos calcular a energia cinética da nossa partícula nesse ponto . Se somarmos com a energia potencial , encontramos a energia mecância:
Passo 6
A energia cinética em é:
Já a energia potencial podemos olhar no gráfico:
Assim, conseguimos a energia mecânica da partícula:
Passo 7
Na letra (c), queremos a energia potencial .
Seria mole se fosse só olhar o gráfico, né? Hahah
Mas ele deixa bem claro que não é para fazer isso falando que:
Então, precisamos usar outra estratégia...
Repara que nós temos a taxa de variação da energia potencial:
Essa variação é da energia com relação à posição. Então esse dado mostra quantos Joules a energia potencial variou por metro :
Passo 8
Como temos a taxa de variação naquele trecho reto do gráfico, podemos pegar algum ponto onde conhecemos o valor de e calcular a partir do quanto a energia variou.
Podemos pegar o ponto :
Então, como estamos em uma reta, temos que:
Resposta
(a)
e aponta para o sentido positivo de .
(b)
(c)