Prove as expressões abaixo:
Passo 1
1ª coisa: NÃO PIRA! Vamos com calma ok?
Vamos lembrar o que cada coisa é, ou seja, o que é média e variância ok?
Então jogando nessa fórmula teremos:
Mas você concorda que:
Ou não?
Se não concorda, pensa comigo aqui rapidinho... Imagina um dado ok? Temos alguns possíveis resultados de X certo? Eles são...
E temos que
Sim?
Agora imagina que usamos esse dado em um jogo de tabuleiro, onde temos uma regra que diz:
“O número de casas que o jogador deve avançar é o dobro do número obtido ao jogar os dados mais três casas.”
Opa! E aí? O que ele quis dizer?
Entãão se jogarmos o dado e tiramos:
Nº do dado(X)
Nº de casas(Y)
1
2.1+3
5
2
2.2+3
7
3
2.3+3
9
4
2.4+3
11
5
2.5+3
13
6
2.6+3
15
Então temos novamente seis possibilidades? Podemos andar 5,7,9,11,13 ou 15 casas certo? Então percebe que podemos dizer que a probabilidade de:
E podemos dizer isso para todos? ((:
Então vamos continuar naquela expressão... Onde estávamos mesmo?
Epa! Olha só:

Então
Passo 2
Vamos olhar a outra expressão agora? Mas primeiro vamos relembrar a expressão de variância
Substituindo teremos
Desenvolvendo (produto notável!!!) & substituindo ...
Olhando para simbora desenvolver? Vamos usar a mesma lógica da primeira expressão que deduzimos (:
Substituindo (iii) em (ii)
Cancelando
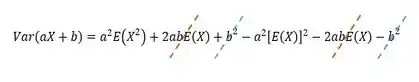
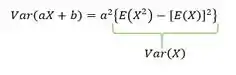
Resposta
Ei, a resposta está no passo a passo :)