1) Seja
Determine o domínio de , os valores de onde a , os valores de onde a se anula e os intervalos onde a é positiva e onde a é negativa.
Passo 1
Vamos lá! Em exercícios como esse, temos muuuuito o que fazer, então é hora de arregaçar as mangas e procurar o domínio. Você sempre vai fazer isso procurando problemas, como no caso, sabemos que dentro da raiz, tem que ser maior que ...
Agora aqui, temos que fazer uma análise de sinal. Vem comigo! ;)
Passo 2
Em casos de produto como esse, analisamos o sinal de um termo que vamos chamar de ...
e o outro termo de ...
Analisar o , que é uma reta, é fazer uma espécie de esboço, e pra isso encontremos o zero da função...
Como a reta é crescente...
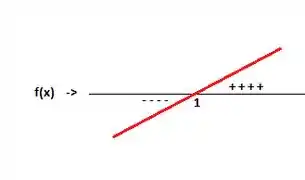
Fazendo o mesmo para a ...
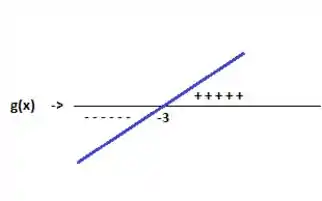
Colocando essas duas retas juntas e fazendo o produto...
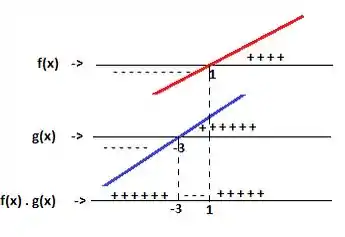
Então percebemos que de até e de pra frente, a raiz
Funciona, pois o termo do interior é positivo (lembre-se de não incluir o e nem o ), pois se não vai zerar, e vamos ter um zero no denominador, heim! ;)
Passo 3
Mas calma que ainda não acabou a análise do domínio, porque apenas analisamos o denominador
Mas ainda falta esse logaritmo natural aí, afinal, se você se recordar, o logaritimando (cara que está dentro do logaritmo) deve ser maior que zero para existir...
Por ser uma inequação equação do segundo grau, devemos primeiro resolver a equação, e depois fazer uma análise semelhante a que fizemos no passo anterior... Por um esboço:
Por ser uma parábola de concavidade pra cima...
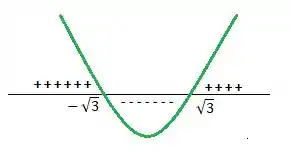
Então para funcionar o logaritmo, devemos ter um acima de e abaixo de (não inclui esses números).
Passo 4
Juntando as duas restrições do passo e do passo , lembrando que é um número um pouco maior que ...
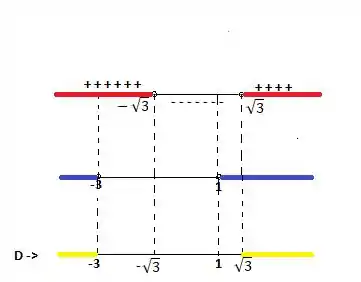
O Domínio como pode ver é a junção da restrição do passo 2 com o Passo 3, logo:
Passo 5
Para os valores de , onde se anula...
Isso só acontece se o nominador for
Por propriedade do ...
Como não está no domínio, apenas o zera a função .
Passo 6
E como uma última tarefa, para determinar onde a função é positiva, basta fazer uma análise de sinal (semelhante a que fizemos anteriormente), mas agora não só de onde poderia dar ruim, e sim da função como um todo:
Veja só, sabemos que para a função ser positiva
O deve ser positivo e a raiz positiva. A raiz é sempre positiva então o sinal de depende inteiramente do sinal do logaritmo.
O logaritmo só é positivo quando o logaritimando é maior que ...
Resolvendo essa igualde primeiro, sabemos que ...
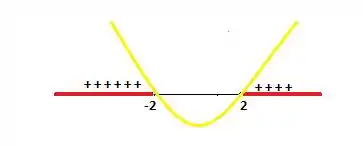
Então o logaritmo é positivo entre e , e também de ao
Como o trecho de até não está no domínio, a função é positiva de
O pedaço de domínio que sobrou para analisar foi o trechinho entre e ...
![]()
Como nesse pedaço, a parábola é negativa, isso significa que o logaritmo é menor que , portanto negativo. Logo a função ...