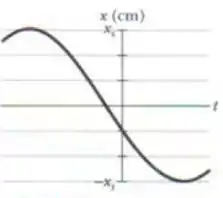
Qual é a constante de fase do oscilador harmônico cuja função posição aparece na figura abaixo, se a função posição é da forma ? A escala do eixo vertical é definida por = 6,0 cm.
Passo 1
Bom, se , cada divisão do gráfico em representa , já que temos 3 divisões da origem até .
Beleza. E para , qual será o valor da função?
Como a curva encontra o eixo na primeira divisão abaixo da origem, temos:
Além disso, olhando no gráfico de novo, vemos que a maior “altura” é
Logo, essa é a amplitude do MHS:
Passo 2
Pra descobrir a fase, então, basta que a gente aplique o valor da função em
Assim, a fase vai ser o arco cujo cosseno é
Mas também podemos ter . E agora, como saber qual o certo?
Passo 3
Podemos ver o seguinte: a derivada da curva num ponto é igual a inclinação da reta tangente naquele ponto, certo?
Então, pegando o ponto , teremos:
Temos que . Como podemos ver na figura, a inclinação da reta tangente é negativa em . Logo, devemos ter:
Assim, concluímos que .