A figura abaixo mostra um gráfico de posição tempo de um oscilador harmônico simples:
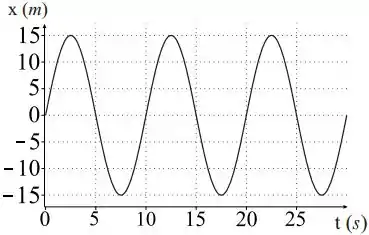
A função que melhor descreve o movimento do oscilador harmônico mostrado no gráfico acima é dada por:
Passo 1
A função nesse caso é
Onde
Passo 2
Pelo gráfico, o período vai ser:
Então:
Além disso, pode-se ver que:
Passo 3
Vamos agora achar o valor da fase.
Basta pegar um valor qualquer da função e resolver a equação. Em :
Então:
Ou:
Precisamos saber qual dos dois casos é o válido.
Passo 4
Vamos pegar outro ponto:
Veja que no ponto . Isso que eu to usando aqui!
Vamos ter:
Como os ângulos que tem cosseno igual a um são e zero, vamos ter:
Podíamos ter também:
Que é o mesmo ângulo, só que um é escrito de forma negativa e outro de forma positiva, mas são equivalentes. Vamos usar a negativa, porque as alternativas não tem . Logo:
Resposta
Letra D