Com base na figura, responda:

Qual o módulo do torque sobre a espira?

Qual é a orientação de equilíbrio da espira?

Para determinar o módulo do torque sobre a espira, vamos começar lembrando da definição de torque:

Adotaremos um sistema de eixos padrão:

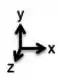
Onde , no nosso caso, temos:

Obs.: A direção e sentido do vetor são determinados pela regra da mão direita.

Agora que temos , precisamos determinar o campo magnético sentido pela espira. O campo magnético gerado por um fio infinito é dado por:

Pela regra da mão direita, vemos que aponta na direção :

Agora que temos e , é só substituir na fórmula do torque e correr pro abraço!