Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento Magnético Dipolar

Ver Teoria
Exercício 512346789101112131415161718192021222324252627282930313233343536373839

Enunciado

A figura abaixo mostra uma bobina retangular de cobre, de 20 espiras, com 10   c m de altura e 5   c m de largura.

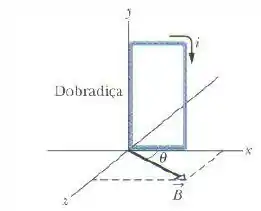
A bobina conduz uma corrente de 0,10   A e dispões de uma dobradiça em um dos lados verticais. Ela está montada no plano x y , fazendo um ângulo de θ = 30 ° com a direção de um campo magnético uniforme de módulo 0,50   T .

Em termos dos vetores unitários, qual é o torque que o campo exerce sobre a bobina em relação à dobradiça?

Passo 1

O torque magnético sobre uma espira é dado por:

τ → = μ → × B →

Então precisamos encontrar cada vetor.

O momento dipolo magnético é dado por:

μ → = n I A →

Onde:

n = 20

I = 0,1   A

A = 0,1 × 0,05 → A = 5 × 10 - 3 m 2

Além disso, utilizando a regra da mão direita, a partir da corrente elétrica, vemos que o momento dipolo magnético está no sentido - k ^ .

Logo:

μ → = 20 × 0,1 × 5 × 10 - 3 - k ^

μ → = 0,01 - k ^   A . m 2

Passo 2

O campo magnético B vale 0,50   T e faz um ângulo de 30 ° com o eixo x , logo, o vetor campo magnético será dado por:

B → = B cos ⁡ ( 30 ° ) i ^ + B sen ⁡ 30 ° k ^

B → = 0,5 × 3 2 i ^ + 0,5 × 1 2 k ^

B → = 3 4 i ^ + 1 4 k ^ T

Passo 3

Agora sim, o torque magnético será dado por:

τ → = μ → × B →

τ → = 0,01 - k ^ × 3 4 i ^ + 1 4 k ^

τ → = 0,0043 - j ^ N . m

Resposta

τ → = 0,0043 - j ^ N . m

Exercícios de Livros Relacionados

Uma esfera uniforme, sólida, uniformemente carregada, de raio R , tem uma densidade volumétrica de carga ρ . A esfera gira em torno de um eixo que passa pelo seu centro com rapidez angular ω . Determi
Uma bobina circular de 160 espiras tem um raio de 1,90 cm. (a) Calcule a corrente que resulta em um momento dipolar magnético de módulo 2,30 A · m 2 . (b) Determine o valor máximo do torque a que a bo
Uma espira circular com 8,0 cm de raio é percorrida por uma corrente de 0,20 A . Um vetor de comprimento unitário, paralelo ao momento dipolar μ → da espira, é dado por 0,60 i ^ – 0,80 j ^ . (Esse vet
Na Fig. 28-50a, duas espiras concêntricas, situadas no mesmo plano, são percorridas por correntes em sentidos contrários. A corrente i 1 na bobina 1 é fixa e a corrente i 2 na bobina 2 é variável. A F
A bobina da Fig. 28-49 conduz uma corrente i = 2,00 A no sentido indicado, é paralela ao plano x z , possui 3,00 espiras, tem uma área de 4,00 × 10 - 3 m 2 e está submetida a um campo magnético unifor