Duas espiras circulares concêntricas, de raios e , estão situadas no plano . Ambas são percorridas por uma corrente no sentido horário, conforme a figura abaixo.
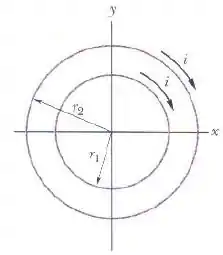
Determine o módulo do momento dipolar magnético do sistema.
Repita o cálculo supondo que a corrente da espira menor mudou de sentido.
Passo 1
Determine o módulo do momento dipolar magnético do sistema.
Nesses casos, o momento dipolar do sistema será a soma de todos os momentos dipolares, logo:
Como as duas correntes estão no mesmo sentido, os momentos dipolares terão o mesmo sinal, logo:
Onde:
Portanto:
Passo 2
Repita o cálculo supondo que a corrente da espira menor mudou de sentido.
A lógica aqui é a mesma, a diferença é que, como as correntes estão em sentidos contrários, os momentos irão ter sinais diferentes, logo:
Substituindo os valores, teremos:
Resposta