Uma espira triangular, de base e altura , contida no plano , é percorrida por uma corrente no sentido horário, conforme a figura abaixo. Na região onde se encontra a espira, existe um campo magnético
onde é uma constante.
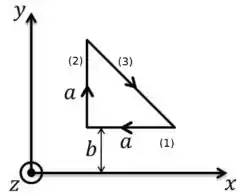
- Calcule o vetor força magnética sobre os lados 1 e 2 da espira.
- Calcule o vetor força magnética sobre o lado 3 da espira.
- Determine o vetor momento de dipolo magnético e o vetor força resultante sobre a espira.
Passo 1
a) A fórmula geral para a força exercida sobre um condutor fechado percorrido por uma corrente na presença de um campo magnético é dada por:
Vamos aplicar essa expressão primeiro para o fio (1), que é paralelo ao eixo . O vetor do condutor pode ser representado por:
Em toda a extensão do fio (1), o campo magnético tem o mesmo valor, já que sua intensidade depende apenas da distância . Portanto, ao longo do fio (1), para o qual temos , o campo magnético tem valor igual a .
Colocando e na expressão para a força, teremos que a força sobre o fio (1) da espira será:
em que utilizamos e fizemos a integral.
Para o fio (2), temos o elemento infinitesimal do condutor escrito como: . Para o fio (2) da espira, o campo magnético tem valores diferentes em todos os pontos de seu comprimento. Por isso, a força sobre esse fio será:
Como , integramos a expressão e obtemos:
Passo 2
b) Como o fio (3) está inclinado, o elemento de comprimento é e o campo magnético varia ao longo de todo o seu comprimento. Por isso, a força total sobre esse condutor será:
Simplificando essa expressão, chegamos a:
Agora aqui, vem um detalhe muito importante!! Você ficaria tentado a jogar o para fora da primeira integral em acima. MAS CUIDADO!!! Nesse caso, e estão relacionados um com o outro, ou seja, se varia, também varia!! Para entender como é a relação entre eles, olha o triângulo abaixo.
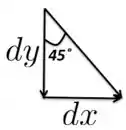
Desse triângulo, a gente tem o seguinte, olhando para a tangente de :
pois . Sacou a ideia?? Isso é o grande lance para matar esse item!!!
Colocando isso lá na integral de e lembrando também que e , a força total no condutor do fio (3) fica:
Passo 3
c) A força resultante sobre a espira é a soma vetorial das forças que encontramos nos passos anteriores, ou seja,
que vai resultar em
Continuando, o momento de dipolo magnético é dado por . Como a corrente está no sentido horário, o vetor área está orientado na direção e sentido , ou seja, entrando no plano da página, o que podemos tirar da regra da mão direita.
Como a área de um triângulo é dada por , temos que o vetor momento de dipolo magnético pode ser representado por: