Um passageiro atrasado que se enconta a uma certa distância do portão de embarque em um aeroporto precisa chegar a ele o mais rapidamente possível. Para tal intento ele considera duas rotas alternativas indicadas na figura por A e B. Na primeira delas (A) ele corre diretamente para uma esteira rolante e continua correndo ao longo dela. A velocidade da esteira em relação ao solo é de . Na segunda (B) ele corre diretamente para o portão. Sabe-se que o comprimento da esteira é de , e que o passageiro, que consegue correr a uma velocidade de , se encontra a 16 metros da esteira. Dentre estas duas alternativas, aquela que levará o passageiro o mais rapidamente ao portão e o tempo necessário para isto será
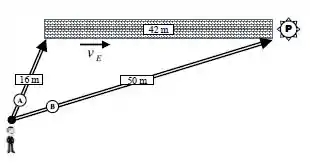
- A rota (A) com
- A rota (B) com
- A rota (A) com
- A rota (B) com
- A rota (A) com
Passo 1
Bom, a primeira parte é entender que ele com toda certeza do mundo vai correr sozinho, sem o auxílio de nada, tanto no caminho quanto no caminho .
Ou seja, o problema é verificar se é mais rápido ele percorrer m na esteira ou a pé.
Caminho A:
Como ele corre e a esteira tem de velocidade, a velocidade total dele será
Caminho :
Ou seja, o caminho A é mais rápido
Só que além dos segundos da esteira ele ainda corre uma parte inicial sozinho, os metros.
Sendo o tempo total então
Resposta
Letra A