Considere a curva , descrita pelo ponto , para , como na figura:
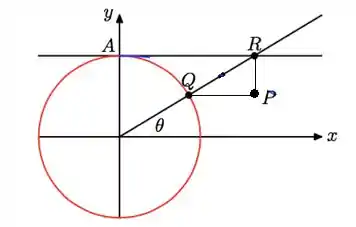
Onde o raio da circunferência é 1.
Uma parametrização de é:
- Nenhuma das demais alternativas.
Passo 1
Para parametrizar a curva , precisamos encontrar as coordenadas do ponto em função do parâmetro . Porque afinal de contas, a curva é o conjunto de todas as posições que o ponto ocupa quando o tá variando de até , sacou?!
O ponto está nesse triangulo aí que tá desenhado na questão. Olhando pra ele, a gente vê que a coordenada do nosso ponto é igual a coordenada do ponto e a coordenada do nosso ponto é igual a coordenada do ponto . Assim
Passo 2
Vamos começar pela coordenada . Já sabemos que:
Mas, o ponto está sobre a circinferencia . Então, a coordenada vai ser a coordenada da parametrização da circunferência, que é então:
Show!
Passo 3
Agora vamos a coordenada .
Pela figura, podemos descobrir a relação que tem com e . Veja que no triângulo de vértices , e , temos que:
E, assim,
Assim, só pra não criar um passo novo, a parametrização da nossa curva vai ficar: