Livro James Stewart, Volume 2, 7ª Edição, Capítulo 13, Seção 2, Exercício 27
(Cap. 13.2 - Ex. 27) Encontre uma equação para a reta tangente à curva de intersecção dos cilindros e no ponto .
Passo 1
Faaala aí, pessoal! Prontos pra resolver mais uma questãozinha? Bora lá então!
O objetivo desse exercício aqui, é encontrar uma equação para a reta tangente, à uma curva de intersecção que será formada entre dois cilindros. Tá, mas o que isso significa?
Quando dois cilindros se cruzarem, teremos a formação de dois círculos:
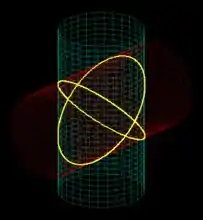
A reta que procuramos, será tangente à essa intersecção mostrada na figura acima.
Bom, agora que a gente sabe o que queremos, como se trata de uma reta tangente à uma curva formada entre os dois cilindros, vamos começar parametrizando essa curva da interseção, e vamos chamar ela de .
A projeção de no plano vai estar contida no círculo:
E nesse momento temos:
Precisamos lembrar que, como temos um círculo, a gente pode parametrizar a partir da função seno e cosseno, o que vai facilitar um pouco a nossa vida! Vamos ficar com:
Tranquilo? Vamos continuar!
Passo 2
Bom, mas o outro cilindro também está contido, né? Então agora é a vez dele!
E nesse caso, próximo do ponto dado, a gente pode ver que:
E por que isso é importante? Porque a partir disso, a gente pode fazer o seguinte:
E como o a gente já descobriu no passo 1, vamos substituir ele na equação acima:
Passo 3
Beleza! Com essas informações, podemos formar a equação vetorial para a nossa intersecção, !! Vale lembrar que essa equação será formada por: .
Como os valores de e foram encontrados nos passos anteriores, basta escrevermos ela aqui:
Passo 4
Agora, a gente precisa fazer a derivada da nossa equação, para poder utilizá-la na fórmula da equação paramétrica que relaciona um ponto dado, com a derivada da equação vetorial: .
Então, fazendo a derivada, vamos ter que:
Ficou meio estranha, né? Mas não se assusta não! Vamos continuar!
Passo 5
Agora, a gente vai fazer uma relação entre o ponto que foi dado no enunciado, com as equações dadas de e . E por que isso? Essa relação vai servir pra gente determinar o tempo para que a curva esteja no ponto .
A relação será a seguinte:
A partir da relação acima, vemos que o ponto corresponde a , então o vetor tangente é:
Opa! Estamos quase lá! Sendo a linha tangente paralela a esse vetor e passando através do ponto , então a nossa equação vetorial para a linha será:
Show de bola, pessoal! Conseguimos!
Pra essa questão era isso! Bora pra mais uma?