Dados o plano
e a reta
Estude a posição relativa de e .
Passo 1
Até agora estávamos estudando a posição relativa entre retas!! Chegou a vez da posição relativa entre reta e plano! Para verificar a posição relativa entre a reta e o plano o enunciado nos dá a equação vetorial do plano e da reta. Com isso, conseguimos retirar os seguintes dados.
Dados:
Passo 2
Pelos dados retirados das equações vetoriais tanto da reta como do plano, temos dois vetores paralelos ao plano. Assim, vamos utilizar a análise entre reta e plano que leva em consideração o produto misto entre o vetor diretor da reta e os vetores do plano.
Assim, primeiro vamos verificar quanto vale o produto misto entre eles. Ressaltando aqui que os vetores do plano não podem ser proporcionais entre si, mas só de olhar para e percebemos que eles não são proporcionais. Bora montar o produto misto!!
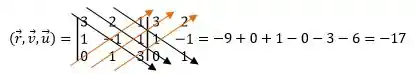
O produto misto deu diferente de ZERO, portanto a reta e o plano são TRANSVERSAIS.