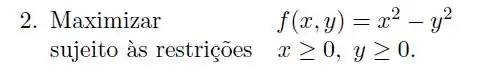
Passo 1
Vamos ver se todas as condições do teorema de Weierstrass são satisfeitas:
Começamos verificando a continuidade da função
É uma função polinomial, então é contínua em todo .
Passo 2
Vamos verificar se o conjunto dado é fechado. Perceba que:
Compreende todo o primeiro quadrante do plano cartesiano. Logo, como o conjunto contém a sua fronteira, o conjunto é fechado.
Passo 3
Verificar se o conjunto é limitado. Não conseguimos encontrar um círculo com centro na origem e com um raio fixo que contenha totalmente o conjunto.
Logo o conjunto não é limitado.
Como as condições do Teorema de Weierstrass não foram todas satisfeitas, podemos afirmar que esse problema não tem solução.
Resposta
Não
Exercícios de Livros Relacionados
Determinar o ponto P(x, y, z) do plano x +3 y +2 z =6 , cuja distância à origem seja mínima.
Determine, pelo método dos mínimos quadrados, a reta que melhor se ajusta aos dados:(1, 2), (0, 0) e (2, 3).
Determine, pelo método dos mínimos quadrados, a reta que melhor se ajusta aos dados:(0,1), (1, 2), (2, 3) e (2, 4).
Uma firma de embalagem necessita fabricar caixas retangulares de 64 cm³ de volume. Se o material da parte lateral custa a metade do material a ser usado para a tampa e para o fundo da caixa, determina
Determinar três números positivos cujo produto seja 100 e cuja soma seja mínima.