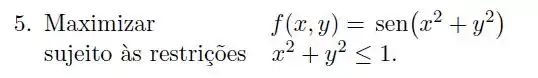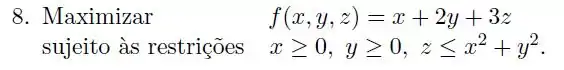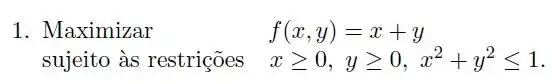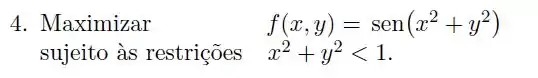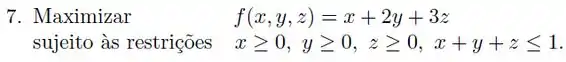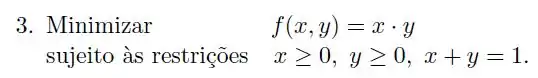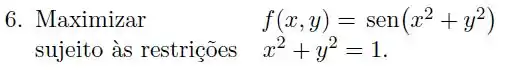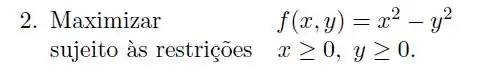Exercícios de Máximos e Mínimos de Funções de Várias Variáveis em Regiões Fechadas - Lista de Exercícios Resolvida
Questão 1
O que podemos afirmar sobre a existência de valores extremos da função
No conjunto ?
Ver solução completaQuestão 2
Podemos garantir que o problema de minimização da função :
Sujeito as restrições , tem solução?
Ver solução completaQuestão 3
Podemos garantir que o problema de maximização da função :
Sujeito as restrições , tem solução?
Ver solução completaQuestão 8
Estude a convergência da série considerando as convergências pontual e uniforme.
Ver solução completaQuestão 13
Considere a função dada por
Onde é o domínio .
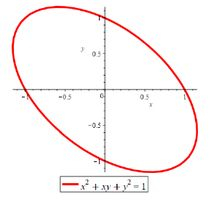
- Encontre e classifique os pontos críticos de no interior do domínio .
- Explique por que os valores extremos absolutos de devem existir em .
- Encontre os valores máximos absolutos e mínimos absolutos de em . Indique os pontos de onde esses valores extremos são atingidos
Questão 14
Considere a função dada por
Onde é o domínio .
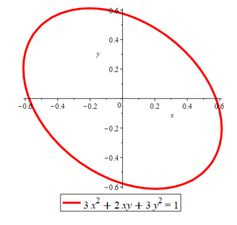
- Encontre e classifique os pontos críticos de no interior do domínio .
- Explique por que os valores extremos absolutos de devem existir em .
- Encontre os valores máximos absolutos e mínimos absolutos de em . Indique os pontos de onde esses valores extremos são atingidos
Questão 15
(2) Considere , definida em todo . Responda:
d) Se pode aplicar o Teorema dos Valores Extremos e garantir a existência de máximo e mínimo globais para (em )?
Ver solução completaQuestão 16
Suponha que f seja uma função contínua no intervalo [a,b]
- f possui máximos e mínimos globais nesse intervalo? Justifique
- Como podemos encontrar esses pontos?
Questão 17
Encontre os valores máximos absolutos e mínimos absolutos da função
No domínio .
Indique onde esses valores extremos são atingidos.
Explique por que esses valores extremos devem existir.
Ver solução completaQuestão 18
Considere a função dada por
Onde é o domínio .
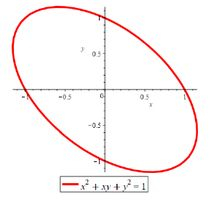
- Encontre e classifique os pontos críticos de no interior do domínio .
- Explique por que os valores extremos absolutos de devem existir em .
- Encontre os valores máximos absolutos e mínimos absolutos de em . Indique os pontos de onde esses valores extremos são atingidos