Uma escada com está apoiada em uma parede e faz um ângulo com o chão. Se o topo da escada está a uma altura de na parede, expresse em termos de e, então, use para estimar a variação em se variar de a .
Passo 1
Bem, ele quer estimar a variação de , para isso, devemos relacionar e e calcular os diferenciais. A situação é que nem a da figura aqui embaixo:
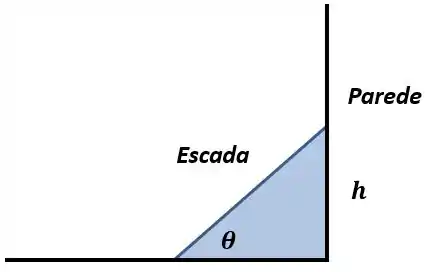
Como temos um triângulo retângulo, podemos fazer
Assim
Agora vamos achar a diferencial,
Agora passamos aquele para direita
Passo 2
Beleza, já sabemos o diferencial, o que falta agora é saber o ângulo e , lembrando que sempre que trabalhamos com ângulos eles precisam estar em radianos.
Repara que o começa em , então esse vai ser o nosso valor de , ele vai funcionar como o ponto de referência como vimos antes. Nessas situações de diferencial, vamos considerar sempre o inicial como o ponto central, beleza?
Agora falta achar , mas lembra da teoria? Nós fazemos a seguinte aproximação:
E esse ele deu no enunciado, que vai ser:
Agora temos que passar esses caras todos para radianos:
Passo 3
Agora vamos achar com tudo que já calculamos antes:
Então:
Assim, com a nossa aproximação, vamos ter: