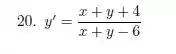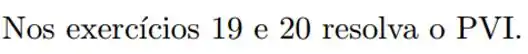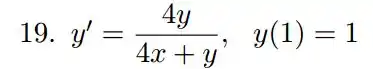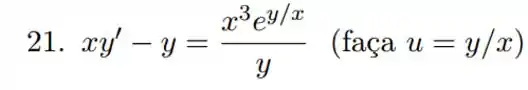Exercícios de EDO com Mudança de Variáveis - Lista de Exercícios Resolvida

Determine a solução geral da equação diferencial:

Resolva a equação diferencial dada usando uma substituição apropriada

Resolva a equação diferencial dada usando uma substituição apropriada

Resolva a equação diferencial dada usando uma substituição apropriada

Sabendo que a equação diferencial que descreve a forma de um fio de densidade linear constante suspenso sob a ação do próprio peso é

Em que é a tensão horizontal no fio em seu ponto mais baixo. Usando a substituição resolva essa equação sujeita à condição inicial

Resolva a seguinte e.d.o por redução de ordem com a substituição :

2) Resolva a equação .

Nos exercícios 19 a 21 use o método desenvolvido na questão 18, para determinar a solução geral das equações.

Considere a equação diferencial

Determine de modo que a mudança de variável transforme a EDO acima em uma equação diferencial linear. NÃO RESOLVA A EDO ACIMA!

Resolva a equação diferencial

Use a substituição para encontrar a solução da e.d.o: