Uma certa quantidade de um gás ideal monoatômico (n moles) está inicialmente à temperatura . Lentamente, sua pressão e seu volume aumentam até dobrarem de valor, de modo que o sistema percorre uma reta no diagrama . Um aluno calculou um calor específico molar para este processo e o chamou de . Indique o ordenamento correto quando o valor de é comparado com e :

(a)

(b)

(c)

(d)

(e)

Vamos lá! Temos algo assim:

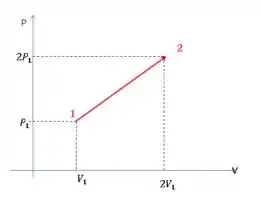
O calor específico molar é o calor específico dividido pelo numero de mols, ok?

Nesse processo, temos

Não sabemos nem o e nem .

Vamos encontrar primeiro a variação da temperatura.

Como é um gás ideal, podemos usar a relação:

Com e

Então

Beleza. Então

Ok!

Agora, vamos pensar em como achar a quantidade de calor trocada entre 1 e 2.

Para isso, vamos imaginar outro caminho. Um isovolumétrico e outro isobárico.

Vamos lá.

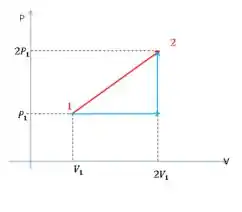
A primeira parte do caminho azul é uma isobárica, então:

E entre esse processo, temos uma variação na temperatura de:

Então

Beleza, agora vamos para a segunda parte do caminho azul, a isovolumétrica:

A variação de temperatura entre esses pontos será

Então

Então o calor necessário para ir de 1 até 2 foi:

Então para o temos que a mesma quantidade de calor será usada para ter essa mesma variação de temperatura.

Como, e , temos que