Exercícios de Energia Interna de um gás e Calores Específicos Molares - Lista de Exercícios Resolvida
Questão 1
Como se altera a energia cinética média de um gás monoatômico ideal quando:
A pressão é duplicada a volume constante?
O volume é duplicado a pressão constante?
Permanece inalterada em ambos os casos.
Cai à metade em ambos os casos.
Dobra em ambos os casos.
Quadruplica e cai a , respectivamente.
Dobra e cai à metade, respectivamente.
Ver solução completaQuestão 2
Dois gases ideais, um monoatômico e um diatômico, sofrem a mesma variação de energia interna. Marque a alternativa verdadeira.
A variação de temperatura, nos dois casos, é a mesma.
A variação de temperatura é maior no gás monoatômico.
A variação de temperatura é maior no gás diatômico.
Não é possível relacionar as variações de temperatura pois não sabemos se o sitema realiza ou não trabalho durante tal processo.
As temperaturas não variam.
Ver solução completaQuestão 3
Fornecemos de calor a um mol de gás diatômico, que se expande a pressão constante. As moléculas do gás giram, mas não oscilam. De quanto a energia interna do gás aumenta?
Ver solução completaQuestão 4
A figura representa a energia térmica de de gás em função da temperatura.
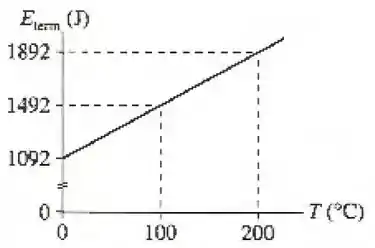
Quanto vale para este gás?
Ver solução completaQuestão 5
Um pesquisador quer estudar o comportamento termodinâmico de sólidos através de uma simulação de computador.
Ele modela um sólido como uma rede cristalina de de átomos ligados aos seus vizinhos por molas ideais.
Contudo, seus “átomos” estão restritos a um plano (ou seja, a simulação é inteiramente bidimensional).
Para testar se sua simulação está bem feita, ele calcula a energia interna do seu sólido.
Qual o valor que ele espera encontrar?
Ver solução completa
Questão 6
De acordo com o teorema da equipartição da energia, a energia térmica de um gás é dividida igualmente entre:
a) as moléculas do gás
b) a energia cinética e a energia potencial do gás
c) a energia cinética de translação e a energia cinética de rotação das moléculas do gás
d) os graus de liberdade das moléculas do gás
e) a temperatura e a pressão do gás
Ver solução completaQuestão 7
Um recipiente contendo hidrogênio (massa molecular ) é posto em contato térmico com um recipiente contendo oxigênio( massa molecular por tempo suficiente para que os dois entrem em equilíbrio térmico. Sobre a energia cinética média e a velocidade média das moléculas de cada gás, podemos afirmar:
- A energia cinética média e a velocidade média são maiores para o oxigênio.
- A energia cinética média é maior para o hidrogênio e a velocidade média é igual para os dois gases.
- A velocidade média é maior para o oxigênio e a energia cinética média é igual para os dois gases.
- A velocidade média é maior para o hidrogênio e a energia cinética média é igual para os dois gases.
Questão 8
Considere os seguintes gases comuns em nossa atmosfera: nitrogênio, com , e oxigênio, com .
Suponha que estes gases estejam em condições de volume, temperatura e pressão nas quais possam ser considerados gases ideais.
Se os gases estão à mesma temperatura, então considere as seguintes afirmativas:
- As moléculas destes gases possuem a mesma energia cinética translacional.
- As moléculas de oxigênio são, em média, mais rápidas que as moléculas de nitrogênio.
- O gás que possui as moléculas com a maior energia cinética translacional é o oxigênio, pois possui maior massa molar.
As CORRETAS são:
- Apenas I.
- Apenas II.
- Apenas III.
- Apenas I e II.
- Apenas II e III.
Questão 9
Marque a afirmativa CORRETA a respeito das propriedades do gás ideal.
- O calor específico a volume constante é maior do que a pressão constante.
- As moléculas do gás são consideradas partículas e, portanto, sem dimensão.
- Num processo adiabático, o trabalho realizado pelo sistema não depende da variação de temperatura.
Questão 10
Um gás ideal é levado do estado A ao estado B pelo processo mostrado no diagrama PV abaixo. Qual das respostas abaixo mais se aproxima do valor da quantidade de calor absorvida pelo gás no processo.
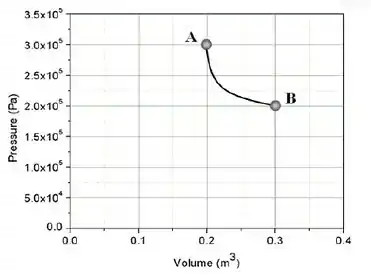
- zero
- Não é possível determinar porque o número de mols n não foi dado.
Questão 11
Num processo termodinâmico, a energia térmica de um sistema num recipiente com paredes adiabaticamente isoladas decresce de 800 J. Qual das afirmações é correta?
- O sistema perdeu 800 J por transferência de calor para o ambiente
- O sistema ganhou 800 J por transferência de calor do ambiente
- O sistema realizou 800 J de trabalho sobre o ambiente
- O ambiente realizou 800 J de trabalho sobre o sistema
- O sistema recebeu 800 J de calor do ambiente e realizou 800 J de trabalho sobre o ambiente
Questão 12
Considere um recipiente com uma mistura de três gases ideais inertes. Sejam , e as capacidades térmicas molares a volume constante de cada um dos gases e suponha que no recipiente haja , e moles de cada um dos gases, respectivamente. Podemos afirmar, então, que a capacidade térmica efetiva de toda a mistura é:
Questão 13
A diferença entre as capacidades térmicas molares a pressão e volume constante , respectivamente, é maior para que tipo de gás?
- Monoatômico.
- Diatômico sem vibração.
- Diatômico com vibração.
- Poliatômico.
- O valor é o mesmo para todos os casos anteriores.
Questão 14
Um cilindro de oxigênio para uso hospitalar contém este gás à pressão de e à temperatura de . Considerando o gás ideal, calcule:
- A energia cinética média de translação por molécula do gás.
- A velocidade quadrática média das moléculas no gás..
- A energia interna por mol do gás.
- A densidade do gás no cilindro.
- Calcule o número de mols num cilindro de , nas condições de temperatura e pressão acima.
Dados:
Ver solução completaQuestão 15
Se um gás ideal monoatômico com N moléculas está em equilíbrio térmico com um gás diatômico com o mesmo número de moléculas e o equilíbrio térmico é mantido quando a temperatura aumenta, a razão entre as variações da energia interna dos dois gases, / é:
a) 5/3;
b) 1;
c) 1/2;
d) 3/5;
e) 2;
Ver solução completaQuestão 16
Das afirmações que seguem, diga quais são verdadeiras: (i) Em um gás ideal o módulo da velocidade de uma molécula é inalterado após uma colisão dessa molécula com as paredes do recipiente que contem o gás. (ii) Num gás ideal não há uma energia potencial de interação entre as suas moléculas. (iii) A energia interna de um gás ideal é proporcional à sua temperatura e inversamente proporcional à sua pressão.
- Apenas (i).
- Apenas (ii).
- Apenas (iii).
- Apenas (i) e (ii).
- Apenas (i) e (iii).
- Apenas (ii) e (iii).
- Todas elas.
- Nenhuma delas.
Questão 17
Qual das seguintes afirmações é falsa?
- Quando um sistema vai de um estado para um estado através de vários processos diferentes, a variação de energia térmica do sistema será a mesma para todos os processos.
- A variação da energia térmica de uma dada quantidade de gás ideal depende apenas da sua variação de temperatura.
- Quando um sistema pode ir de um estado para um estado através de vários processos diferentes, a quantidade de trabalho realizado sobre o sistema será a mesma para todos os processos.
- Um processo quase-estático é aquele ao longo do qual o sistema nunca está longe do equilíbrio.
- Para qualquer substância que se expande quando aquecida, .
Questão 18
Uma amostra de 4,0 g de um gás monoatômico de massa molar a uma temperatura inicial de interage termicamente com de um gás diatômico de massa molar a uma temperatura inicial de , conforme mostra a figura abaixo.
As Energias térmicas iniciais dos gases monoatômico e diatômico, respectivamente, são
Questão 19
Uma amostra de 4,0 g de um gás monoatômico de massa molar a uma temperatura inicial de interage termicamente com de um gás diatômico de massa molar a uma temperatura inicial de , conforme mostra a figura abaixo.
A temperatura final de equilíbrio é aproximadamente
- 333 K
- 338 K
- 311 K
- 304 K
- 300 K
Questão 20
Quando de energia são transferidos na forma de calor a certo gás ideal sujeito à pressão atmosférica (), seu volume aumenta para .
- Calcule a variação da energia interna do gás.
- Calcule o calor específico molar a volume constante deste gás. Expresse seu resultado em termos de (constante universal dos gases).
- Supondo que as partículas constituintes do gás não vibram, calcule o número de graus de liberdade de suas partículas e em seguida determine se este gás é () monoatômico, () diatômico ou () poliatômico.
Questão 21
Dois gases ideais, um monoatômico e um diatômico, sofrem a mesma variação de energia interna. Marque a alternativa verdadeira.
- A variação de temperatura, nos dois casos, é a mesma.
- A variação de temperatura é maior no gás monoatômico.
- A variação de temperatura é maior no gás diatômico.
- Não é possível relacionar as variações de temperatura pois não sabemos se o sitema realiza ou não trabalho durante tal processo.
- As temperaturas não variam.
Questão 22
Das afirmações que seguem, diga quais são verdadeiras: (i) Em um gás ideal o módulo da velocidade de uma molécula é inalterado após uma colisão dessa molécula com as paredes do recipiente que contem o gás. (ii) Num gás ideal não há uma energia potencial de interação entre as suas moléculas. (iii) A energia interna de um gás ideal é proporcional à sua temperatura e inversamente proporcional à sua pressão.
- Apenas (i).
- Apenas (ii).
- Apenas (iii).
- Apenas (i) e (ii).
- Apenas (i) e (iii).
- Apenas (ii) e (iii).
- Todas elas.
- Nenhuma delas.
Questão 23
- Os gráficos abaixo representam diferentes funções da energia de um gás . O gráfico que pode ser usado para representar adequadamente o comportamento da energia interna de de um gás ideal em função do produto da pressão pelo volume de gás é:
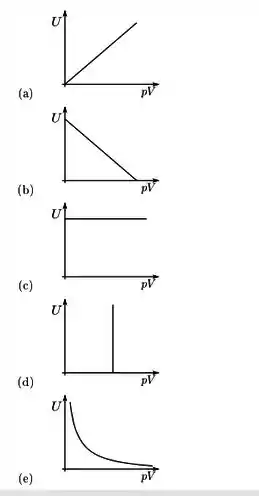
Questão 24
Como se altera a energia cinética média de um gás monoatômico ideal quando a pressão é duplicada a volume constante?
E quando o volume é duplicado a pressão constante?
- Permanece inalterada em ambos os casos.
- Cai à metade em ambos os casos.
- Dobra em ambos os casos.
- Quadruplica e cai a , respectivamente.
- Dobra e cai à metade, respectivamente.
Questão 25
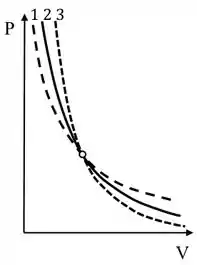
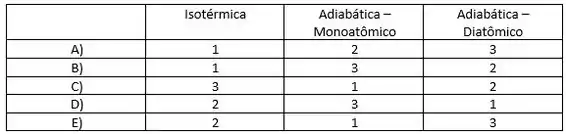
A figura ao lado mostra um diagrama PV, no qual estão assinaladas 3 curvas possíveis que passam por um mesmo ponto (representado pelo círculo). Uma dessas curvas representa uma transformação isotérmica de um gás ideal, e as outras duas transformações adiabáticas, sendo uma delas a curva adiabática seguida por um gás ideal monoatômico, e a outra a seguida por um gás ideal diatômico. Sendo 1 = curva tracejada; 2 = curva cheia; 3 =
curva tracejada fina, identifique qual curva corresponde a qual processo.
Questão 26
Um mol de um gás ideal monoatômico pode atingir o mesmo estado final através de três processos distintos como mostrado no gráfico abaixo.
Dados e .
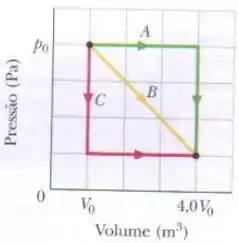
A variação de energia térmica no processo A é:
A) 0 J
B) -3,0 J
C) -37,5 J
D) 37,5 J
E) 24,9 J
Ver solução completaQuestão 27
(Capítulo 19.Exercícios – Ex. 26) Quando uma quantidade de gás monoatômico ideal se expande a uma pressão constante de , o volume do gás aumenta de para . Qual é a variação da energia interna do gás?
Ver solução completaQuestão 28
(Capítulo 19.Exercícios – Ex. 10) Cinco moles de um gás ideal monoatômico com uma temperatura inicial de se expandem e, nesse processo, absorvem 1200 J de calor e realizam 2100 J de trabalho. Qual é a temperatura final do gás?
Ver solução completaQuestão 29
(Capítulo 19.Exercícios – Ex. 19) Ebulição da água sob pressão elevada. Quando a água entra em ebulição sob a pressão de 2,0 atm, o calor de vaporização é , e o ponto de ebulição é . A essa pressão, 1,0 kg de água possui volume igual a , e 1,0 kg de vapor d’água possui volume igual a . a) Calcule o trabalho realizado quando se forma 1,0 kg de vapor d’água nessa temperatura. b) Calcule a variação da energia interna da água.
Ver solução completaQuestão 30
Supondo que o hélio se comporta como um gás ideal monoatômico, se 2 mols de hélio sofreram um aumento de temperatura de 100 K a pressão constante, a energia transferida para o gás na forma de calor foi de aproximadamente:
a) 2.500 J;
b) 1.700 J;
c) 4.200 J;
d) 5.000 J;
e) 6.700 J;
Ver solução completaQuestão 31
(Capítulo 19.Exercícios – Ex. 15) Um gás ideal evolui do estado para o estado no diagrama mostrado na Figura 19.22. Durante esse processo, 400 J de calor são fornecidos, e a pressão dobra. a) Quanto trabalho é realizado pelo gás, ou sobre ele? Explique. b) Compare a temperatura do gás em com a sua temperatura em . Seja especifico. c) Compare a energia interna do gás com com a energia interna em . Novamente, seja específico, e explique.
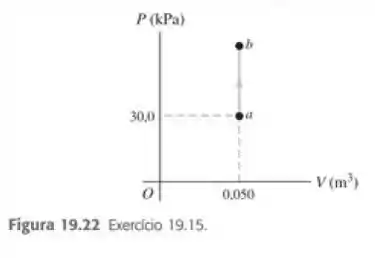
Questão 32
(Capítulo 19.Exercícios – Ex. 9) Um gás no interior de um cilindro se expande de um volume igual a 0,110 até um volume igual a . O calor flui para dentro do sistema com uma taxa suficiente para manter a pressão constante e igual a durante a expansão. O calor total fornecido ao sistema é igual a . a) Calcule o trabalho realizado pelo gás. b) Calcule a variação da energia interna do gás. c) O resultado depende ou não do gás ser ideal? Justifique sua resposta.
Ver solução completaQuestão 33
(Capítulo 19.Exercícios – Ex. 21) Um cilindro contém do gás dióxido de carbono () à temperatura de . O cilindro possui um pistão sem atrito, que mantém sobre o gás uma pressão constante igual a . O gás é aquecido e sua temperatura aumenta para . Suponha que o possa ser considerado um gás ideal. a) Desenhe um diagrama para esse processo. b) Qual é o trabalho realizado pelo gás nesse processo? c) Sobre o que esse trabalho é realizado? d) Qual é a variação de energia interna do gás? e) Qual é o calor fornecido ao gás? f) Qual seria o trabalho realizado se a pressão fosse igual a ?
Ver solução completaQuestão 34
(Capítulo 19.Exercícios – Ex. 30) O gás propano se comporta como um gás ideal com . Determie o calor especifico molar a volume constante e o calor especifico molar à pressão constante.
Ver solução completaQuestão 35
Um gás inicialmente a 2.0 atm de pressão e 127°C é comprimido a temperatura constante até o seu volume cair à metade. Em seguida expande a pressão constante, até seu volume retornar ao valor inicial. Qual a temperatura final do gás?
A) 254°C
B) 527°C
C) A resposta depende se o gás é monoatômico ou diatômico
D) 127°C
E) -73°C
Ver solução completaQuestão 36
. Um gás ideal poliatômico contendo mols tem sua temperatura aumentada de para a pressão constante. Determine o trabalho realizado pelo gás e a energia média (translação rotação) por molécula do gás no final do processo termodinâmico. Considere a constante de Boltzmann .
. e
. e
. e
. e
. e
. Nenhuma das alternativas
. e
Ver solução completaQuestão 37
O ponto na figura representa o estado inicial de um gás ideal e a isoterma que passa pelo ponto divide o diagrama p-V nas regiões 1 e 2. Assinale a alternativa correta a respeito da variação da energia interna ΔEint nos seguintes processos:
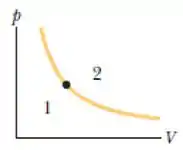
a) ΔEint é negativa se o estado do sistema se move para qualquer ponto da região 1 e ΔEint é positiva se o estado do sistema se move para qualquer ponto da região 2;
b) ΔEint é positiva se o estado do sistema se move para qualquer ponto da região 1 e ΔEint é negativa se o estado do sistema se move para qualquer ponto da região 2;
c) ΔEint é negativa se o estado do sistema se move para baixo na curva isoterma;
d) ΔEint é positiva se o estado do sistema se move para baixo na curva isoterma;
e) ΔEint é nula se o estado do sistema se move para qualquer ponto da região 1 ou da região 2;
Ver solução completaQuestão 38
Dois recipientes com gases monoatômicos e estão em bom contato térmico entre si há um tempo muito longo, mas bem isolados da sua vizinhança (fig).
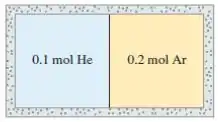
Sobre o valor atual das velocidades quadráticas médias de cada gás, e suas energias cinéticas médias de translação , podemos afirmar:
Questão 39
Para aumentar em a temperatura de uma amostra de gás ideal, são necessários de calor quando o gás é mantido a volume constante, e quando o gás é mantido a pressão constante. Quantos mols de gás estão presentes?
Dados:
Ver solução completaQuestão 40
Das afirmações a seguir, quais delas são verdadeiras? (i) Em um gás ideal o módulo da velocidade das moléculas é inalterado imediatamente após elas colidirem com as paredes do recipiente que as contém. (ii) Num gás ideal não há energia potencial de interação entre as suas moléculas. (iii) A energia interna de um gás ideal é sempre diretamente proporcional à sua temperatura e inversamente proporcional à sua pressão.
(a) Apenas (i).
(b) Apenas (ii).
(c) Apenas (iii).
(d) Apenas (i) e (ii).
(e) Apenas (i) e (iii).
(f) Apenas (ii) e (iii).
(g) Todas elas.
(h) Nenhuma delas.
Ver solução completaQuestão 41
Uma casa tem paredes bem isoladas termicamente com as janelas e portas fechadas (nenhum gás está escapando ou entrando). Tem um volume de de ar a , com uma pressão de Pa.
(a) Calcule a energia (em forma de calor) necessária para aumentar a temperatura do gás diatômico ideal (5 graus de liberdade) por . Fornecer a expressão e o valor.
(b) Se toda essa energia pudesse ser usada para levantar um objeto de massa a uma altura de , qual seria o valor de ? Fornecer a expressão e o valor.
(c) Qual seria o valor de m se fosse um gás monoatômico? Fornecer a expressão e o valor.
Ver solução completaQuestão 42
Considere as três afirmativas abaixo, a respeito de um gás IDEAL:
- A energia interna de um gás ideal depende diretamente de seu volume
- O calor específico à pressão constante de um gás ideal é sempre menor que à volume constante.
- O calor específico a volume constante de um gás ideal é função apenas da temperatura.
Marque a alternativa que indica as afirmativas CORRETAS:
- I
- II
- III
- I e II
- I e III
- II e III
- Todas estão corretas.
- Nenhuma está correta.
Questão 43
7 - Uma caixa cúbica com lados de contém moléculas de gás Hélio, com uma velocidade quadrática média de . A massa de uma molécula de Hélio é Qual é a pressão média exercida pelas moléculas nas paredes do recipiente? A constante de Boltzmann é e a constante de gás ideal é .
Questão 44
Uma certa quantidade de um gás ideal monoatômico (n moles) está inicialmente à temperatura . Lentamente, sua pressão e seu volume aumentam até dobrarem de valor, de modo que o sistema percorre uma reta no diagrama . Um aluno calculou um calor específico molar para este processo e o chamou de . Indique o ordenamento correto quando o valor de é comparado com e :
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 45
Com relação às previsões da Teoria Cinética dos Gases Ideais e do teorema da equipartição de energia para o calor específico molar a volume constante , podemos afirmar que:
(a) para os gases monoatômicos , independente da temperaura e pode variar a para os gases diatômicos, dependendo da temperatura.
(b) para todos os gases, independentemente da temperatura.
(c) para os gases monoatômicos e para os gases diatômicos, independentemente da temperatura.
(d) Para todos os gases pode variar em função da temperatura.
Ver solução completaQuestão 46
Dois recipientes com gases monoatômicos 4 He e 40 Ar estão em bom contato térmico entre si há um tempo muito longo, mas bem isolados da sua vizinhança (fig).
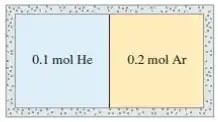
Sobre a energia térmica total e a temperatura final de cada gás, podemos afirmar que:
a)
b)
c)
d)
e)
Ver solução completaQuestão 47
Um pesquisador quer estudar o comportamento termodinâmico de sólidos através de uma simulação de computador.
Ele modela um sólido como uma rede cristalina de de átomos ligados aos seus vizinhos por molas ideais.
Contudo, seus “átomos” estão restritos a um plano (ou seja, a simulação é inteiramente bidimensional).
Para testar se sua simulação está bem feita, ele calcula a energia interna do seu sólido.
Qual o valor que ele espera encontrar?
Questão 48
Um pesquisador quer estudar o comportamento termodinâmico de sólidos através de uma simulação de computador. Ele modela um sólido como uma rede cristalina de N = 1 bilhão de átomos ligados aos seus vizinhos por molas ideais. Contudo, seus “átomos” estão restritos a um plano (ou seja, a simulação é inteiramente bidimensional). Para testar se sua simulação está bem feita, ele calcula a energia interna do seu sólido. Qual o valor que ele espera encontrar?
(a) = (1/2)NT.
(b) = NT.
(c) = (3/2)NT.
(d) = (5/2)NT.
(e) = 2NT.
(f) = 3NT.
(g) = (7/2)NT.
Ver solução completa