Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Interna de um gás e Calores Específicos Molares

Ver Teoria
Exercício 381234567891011121314151617181920212223242526272829303132333435363739404142434445464748

Enunciado

Dois recipientes com gases monoatômicos H e 4 e A r 40 estão em bom contato térmico entre si há um tempo muito longo, mas bem isolados da sua vizinhança (fig).

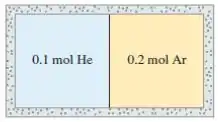
Sobre o valor atual das velocidades quadráticas médias v r m s de cada gás, e suas energias cinéticas médias de translação ε , podemos afirmar:

  1. v H e > v A r   e   ε H e = ε A r
  2. v H e < v A r   e   ε H e = ε A r
  3. v H e = v A r   e   ε H e = ε A r
  4. v H e > v A r   e   ε H e ≠ ε A r
  5. v H e < v A r   e   ε H e ≠ ε A r

Passo 1

Temos que a energia cinética média de translação de um gás ideal monoatômico é

ε m e d = 1 2 m v r m s 2 = 3 2 k B T

Passo 2

As energias cinéticas médias dos gases serão:

ε H e = 3 2 k B T H e

ε A r = 3 2 k B T A r

Como os dois recipientes tem um bom contato térmico, depois de um tempo muito longo, suas temperaturas vão se igualar,

T H e = T A r

Então

ε H e = ε A r

Passo 3

Para descobrir as velocidades, vamos usar a expressão

ε = 1 2 m v r m s 2

v r m s = 2 ε m

Então, como as energias são iguais:

v H e v A r = 2 ε / m H e 2 ε / m A r = m A r m H e

Vamos calcular as massas, segundo a equação

m = n   M

Onde M é a massa molar.

m H e = n H e M H e = 0,1 ∙ 4 = 0,4   g

m A r = n A r M A r = 0,2 ∙ 40 = 8   g

v H e v A r = 8 0,4 = 20 > 1  

Então,

v H e > v A r

Resposta

a)   v H e > v A r   e   ε H e = ε A r

Exercícios de Livros Relacionados

O invólucro e a cesta de um balão de ar quente têm um peso total de 2,454k N e o invólucro tem uma capacidade (volume) de 2,18.10 3m 3 . Qual deve ser a temperatura do ar no interior do invólucro, qua
Um recipiente contém uma mistura de três gases não reagentes: 2,40 mol do gás 1 com C V 1 = 12,0J / m o l . K , 1,50m o l do gás 2 com C V 2 = 12,8J / m o l . K e 3,20m o l do gás 3 com C V 3 = 20,0J
A temperatura de 2,00m o l s de um gás ideal monoatômico é aumentada de 15,0K a volume constante. Determine (a) o trabalho W realizado pelo gás, (b) a quantidade Q de calor transferida para o gás, (c)
A massa da molécula de um gás pode ser calculada a partir do calor específico a volume constante c V . (Note que não se trata de C V ) Tome c V = 0,075c a l / g ° C para o argônio e calcule (a) a mass
Fornecemos 70J de calor a um gás diatômico, que se expande a pressão constante. As moléculas do gás giram, mas não oscilam. De quanto a energia interna do gás aumenta?