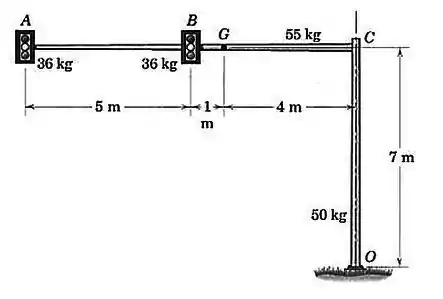
Calcule as forças e o momento de reação na base aparafusada da estrutura de sinal de trânsito suspenso. Cada sinal tem uma massa de , enquanto que as massas dos elementos e são e , respectivamente.
Passo 1
O diagrama de corpo livre pode ser representado por:
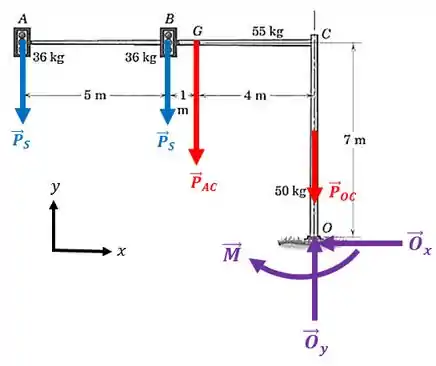
Passo 2
Vamos calcular as forças peso que estão no diagrama:
E vetorialmente, temos que a força peso do sinal aponta para baixo, então:
A força peso da barra é:
E o vetor é:
E por último o peso da barra :
Transformando em vetor temos:
Passo 3
Agora vamos achar as reações de apoio. Perceba que o apoio é um engaste, pois a estrutura não pode se movimentar em nenhuma direção e nem girar. Inclusive foi dito no enunciado que a base é aparafusada.
Vamos começar usando o equilíbrio de momentos em relação ao ponto e considerando o sentido de giro anti-horário como positivo, temos:
Repare que a força não tem braço de alavanca com relação ao ponto . Então, vamos substituir os valores:
Esse momento é positivo, ou seja, ele gira no sentido horário.
Passo 4
Perceba que não há forças horizontais além da reação de apoio , então:
Agora vamos fazer o equilíbrio das forças verticais: