O elemento e a roldana em , juntos, têm uma massa de , com um centro de massa combinado em . Calcule o módulo da força suportada pela conexão de pino em quando a carga de é aplicada. O colar em só pode dar apoio na direção horizontal.
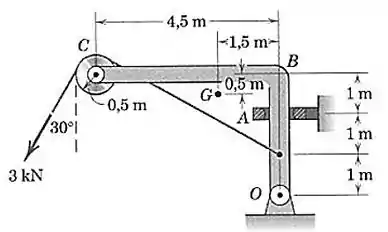
Passo 1
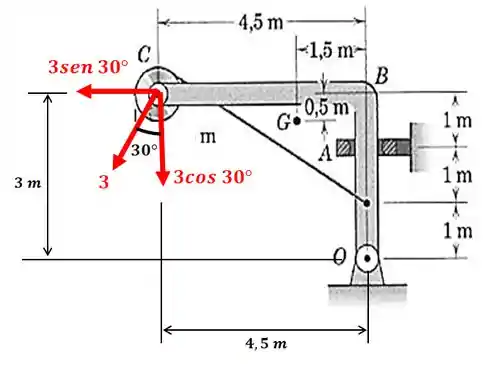
O diagrama de corpo livre desta estrutura fica assim:
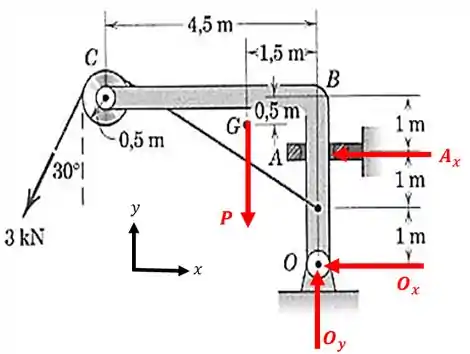
Repare que o colar em só impede o movimento na direção horizontal, então colocamos uma reação horizontal neste ponto.
Já o apoio em impede os movimentos horizontal e vertical, por isso colocamos duas reações sendo uma em cada direção.
Passo 2
Vamos começar fazendo o somatório de momentos com relação ao ponto , porque assim conseguimos achar o valor da reação :
Mas repare que temos uma força inclinada de ... Vamos levar esta força para o centro da roldana. Mas quando levamos a força, sempre temos que levar o momento que ela faz com relação ao ponto:
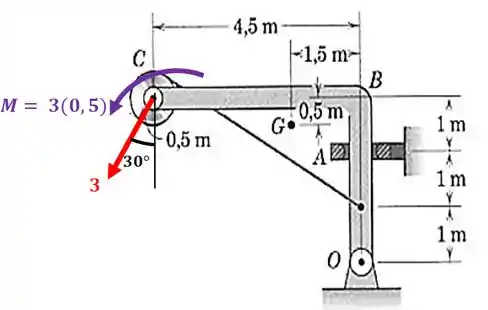
Esse momento surgiu devido ao braço de alavanca com relação ao centro da roldana ser de , assim:
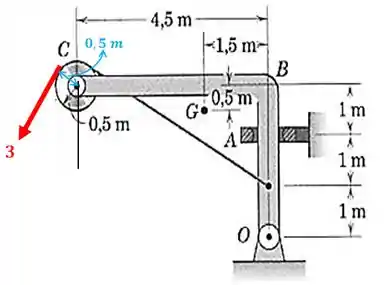
Beleza?
Agora sim podemos achar as componentes vertical e horizontal da força de :
Passo 3
Vamos achar o módulo da força peso:
Passando tudo para a mesma unidade:
Então, temos:
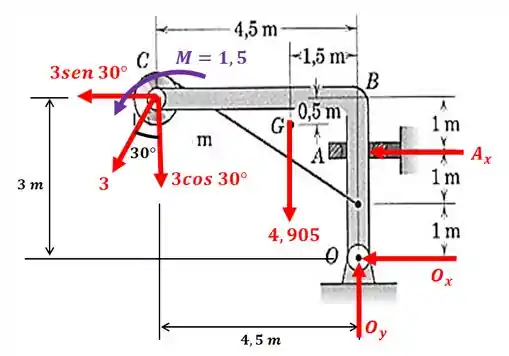
Agora sim podemos calcular o momento, considerando o sentido anti-horário como positivo:
Repare que achamos uma força com sinal negativo, isso porque arbitramos o sentido contrário para a reação no diagrama de corpo livre. Na verdade, deve ser assim:
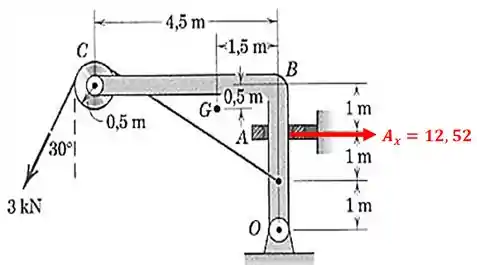
Passo 4
Agora vamos fazer o somatório de forças horizontais:
Passo 5
E para finalizar vamos fazer o somatório de forças verticais:
Passo 6
Vamos calcular a resultante das forças no ponto :