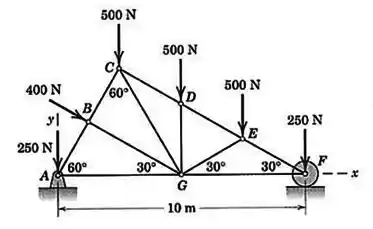
Determine as reações externas em e para a treliça de um telhado carregada como mostrado. As cargas verticais representam o efeito de sustentação dos materiais do telhado, enquanto a força de representa uma carga devida ao vento.
Passo 1
O diagrama de corpo livre dessa treliça fica assim:
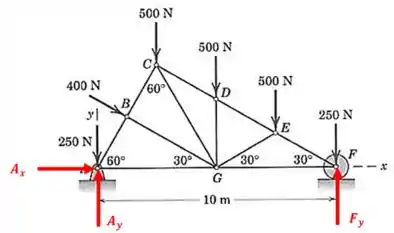
Perceba que o apoio impede o movimento tanto na vertical quanto na horizontal, por isso tem duas reações de apoio. Já o apoio em é um rolete, ou seja, permite que a estrutura se mova na horizontal, mas impede o movimento na vertical.
E não esqueça que só colocamos reação de apoio na direção em que há o impedimento de movimento.
Passo 2
Para achar as reações, temos que começar fazendo o somatório de momentos com relação a um ponto. Mas qual ponto vamos escolher?
Temos que escolher um ponto que tenha uma das nossas incógnitas, ou seja, o ponto ou . Dessa forma, eliminamos uma das incógnitas, já que a força que está bem em cima do ponto que escolhermos não possui braço de alavanca.
Vamos escolher o ponto .
Repare que não temos as distâncias da maioria das forças... Então, vamos achar!
Passo 3
Vamos começar separando os triângulos que formam a treliça e achando seus ângulos. Vamos começar por este aqui:
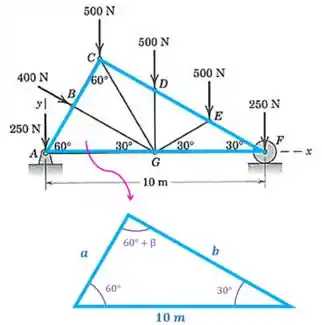
A gente sabe que a soma de todos os ângulos internos de um triângulo é igual a , então o ângulo será:
Então, temos o seguinte triângulo:
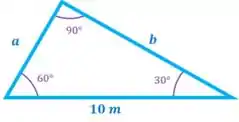
Vamos usar a lei dos senos para achar o valor do lado :
Como o triângulo é retângulo, pois tem um ângulo de , vamos usar o Teorema de Pitágoras para achar o lado :
Vamos passar para outro triângulo.
Passo 4
Agora vamos pegar esse triângulo aqui:
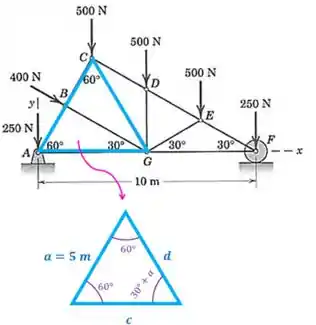
O ângulo será:
Como este triângulo tem todos os ângulos iguais a ele é um triângulo equilátero. Lembra deste triângulo? Ele tem todos os lados iguais. Ou seja, todos os lados do nosso triângulo serão iguais a :
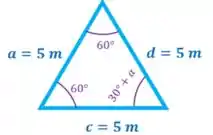
Passo 5
Agora vamos achar a distância das forças com relação ao ponto que ainda não sabemos:
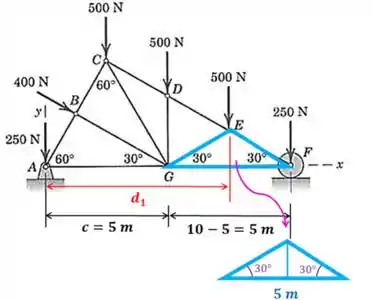
Para achar a distância vamos usar o triângulo destacado na figura. Precisamos saber quanto vale metade da sua base. Mas repare que esse triângulo é isósceles, pois tem os dois ângulos iguais. Você lembra o que é triângulo isósceles? É aquele que tem dois lados iguais.
Então:
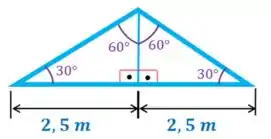
Agora conseguimos achar a distância :
Beleza?
Passo 6
Vamos a achar a distância agora:
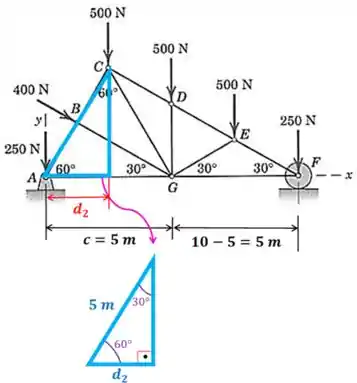
Vamos usar trigonometria para achar a distância :
Passo 7
Agora só falta achar a distância da força de . Mas repare que esta força está inclinada, então vamos começar decompondo-a:
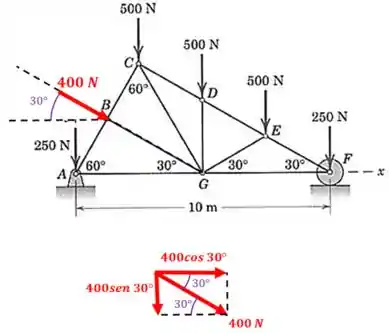
Agora vamos achar as distâncias dessas duas componentes até o ponto :
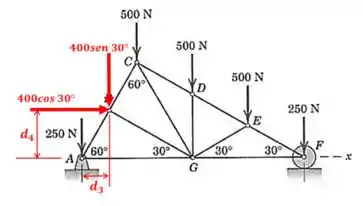
Para isso, vamos começar usando semelhança de triângulos com dois triângulos que tem ângulos internos iguais, são eles:
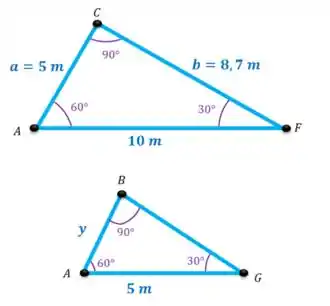
Então:
Agora conseguimos achar as distâncias e :
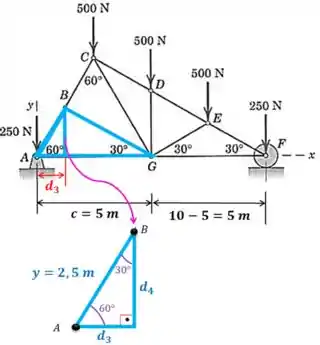
Vamos usar trigonometria para achar :
Agora vamos achar :
Pronto, temos todas as distâncias!!!!
Passo 8
Agora sim podemos calcular o somatório de momento com relação ao ponto . Para isso vamos considerar o momento positivo no sentido anti-horário:
Passo 9
Agora vamos fazer o somatório de forças horizontais:
Repare que o sinal deu negativo. Isso significa que arbitramos o sentido da reação ao contrário no diagrama de corpo livre. Ou seja, está apontando para o sentido negativo do eixo .
Passo 10
Agora vamos fazer o equilíbrio das forças verticais: