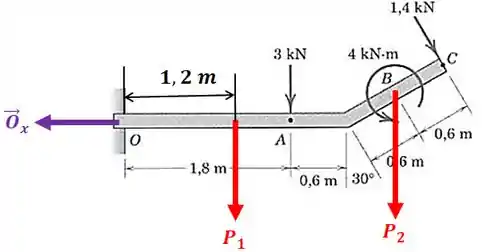
A viga uniforme tem massa de por metro de comprimento. Calcule as reações no apoio . As cargas mostradas estão em um plano vertical.
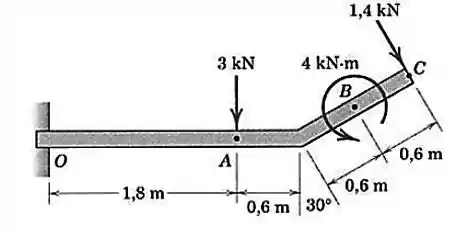
Passo 1
O diagrama de corpo livre pode ser representado por:
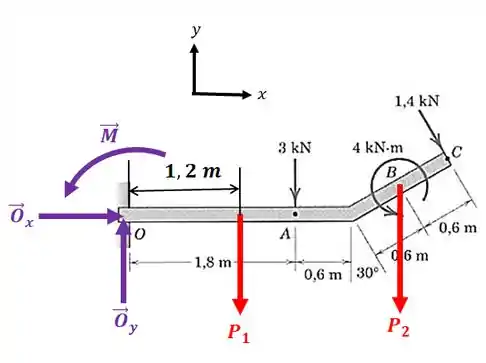
Perceba que o apoio é um engaste, então tem reações horizontal, vertical e o momento.
A força é o peso da barra horizontal e é o peso do trecho correspondente a barra inclinada.
Passo 2
Vamos calcular as forças peso das barras. Como a viga é uniforme e possui por metro de comprimento, a massa da barra horizontal é:
Então, o módulo de é:
Como todas as forças estão em , vamos passar o peso para esta unidade também:
Já a massa da barra inclinada é:
Então, o módulo de é:
Passando para a unidade de , temos que:
Beleza?
Passo 3
Vamos começar usando o equilíbrio de momentos em relação ao ponto :
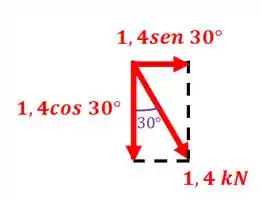
Mas antes vamos decompor aquela força inclinada de :
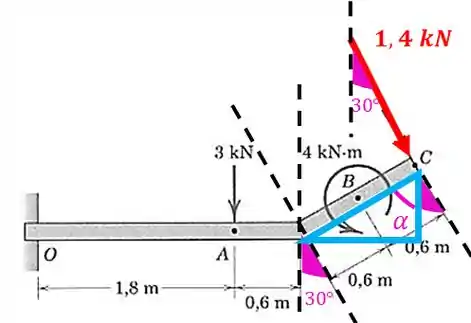
Como o ângulo de inclinação da força é de com relação à vertical, temos que:
Agora vamos usar o triângulo para achar as distâncias com relação ao ponto . Pelo desenho, temos que:
Se um dos ângulos internos de um triângulo retângulo é de , então o outro é :
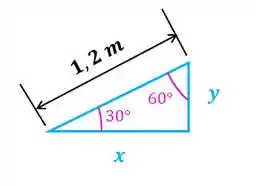
Portanto, o comprimento será:
Este valor será o braço de alavanca da componente horizontal da força de com relação ao ponto :
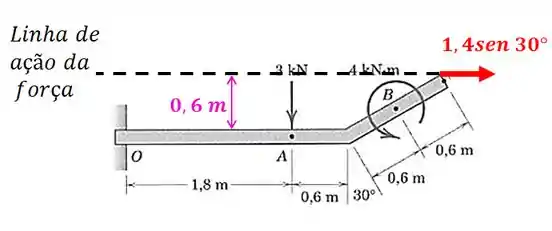
E o comprimento será:
Então, o braço de alavanca da componente vertical da força de com relação ao ponto é de:
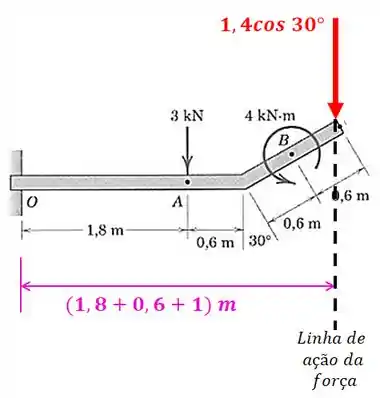
Passo 4
Agora sim podemos calcular o somatório de momento:
Repare que o braço de alavanca do peso da barra inclinada é igual a metade da altura do triângulo:
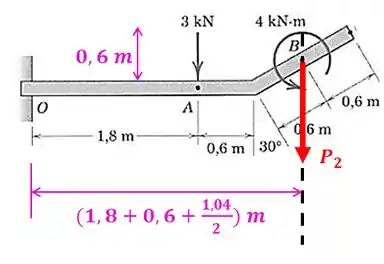
Então, a reação momento será de:
Como o momento deu positivo, indica que arbitramos um sentido correto para a reação de apoio, ou seja, o momento é no sentido anti-horário.
Passo 5
Agora vamos fazer o somatório de forças horizontais:
Repare que o sinal deu negativo, ou seja, arbitramos o sentido contrário para a reação . Dessa forma, esta força aponta para a esquerda (sentido contrário ao que desenhamos antes):
Passo 6
Agora vamos fazer o equilíbrio das forças verticais: