Determine as componentes horizontal e vertical da reação no pino e a reação do colar liso sobre a barra.
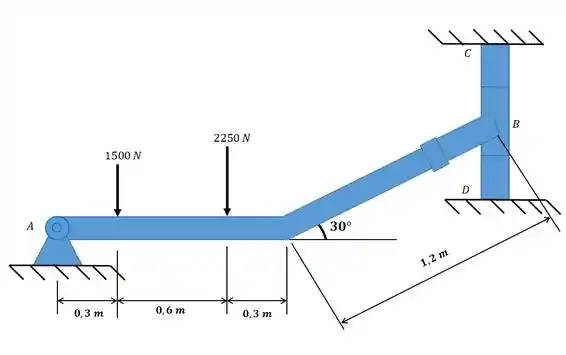
Passo 1
O diagrama de corpo livre dessa estrutura fica assim:
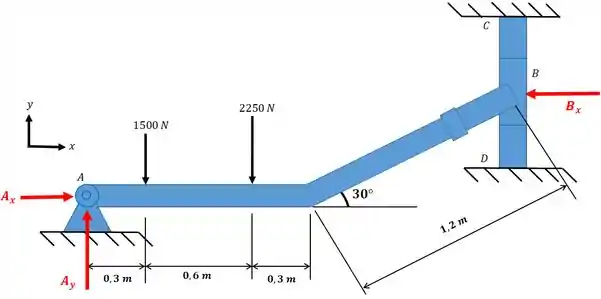
Perceba que o apoio impede o movimento somente na horizontal, por isso tem uma reação de apoio. Já o apoio em impede o movimento tanto na horizontal quanto na vertical.
Passo 2
Para achar as reações, temos que começar fazendo o somatório de momentos com relação a um ponto. Mas qual ponto vamos escolher?
Vamos escolher o ponto .
Passo 3
Vamos achar a distância da reação até o ponto :
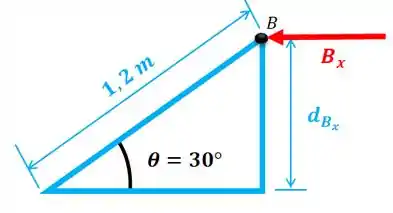
Então:
Passo 4
Agora vamos fazer o somatório de momentos com relação ao ponto considerando o sentido anti-horário como positivo:
Passo 5
Agora vamos fazer o somatório de forças horizontais:
Passo 6
Para finalizar vamos fazer o equilíbrio das forças verticais: