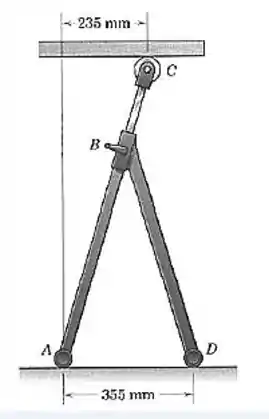
O suporte deslizante é usado para apoiar partes de chapas longas enquanto elas são cortadas por uma série de bancadas. Se a chapa exerce uma força direcionada para baixo de no rolete , determine as ações verticais em e Note que a conexão em é rígida e que os pés e são tubos horizontais razoavelmente longos, com recobrimentos deslizantes.
Passo 1
Fala aí, pessoal!! Vamos entender primeiro o que está acontecendo nessa situação aqui. O suporte deslizante descrito no problema é o próprio conjunto , que desliza no ponto através de um rolete.
Como as barras e são “razoavelmente longas” podemos aproximar as reações em e para forças verticais, como sugerido no enunciado.
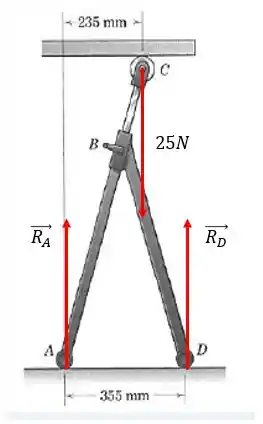
Sabendo disso podemos fazer o sistema de forças, que é dado abaixo:
Passo 2
Temos que satisfazer a duas condições:
E:
Para o caso dos momentos, vamos escolher o ponto , assim não precisamos trabalhar com de cara, pois esta força não tem braço de alavanca com relação ao ponto .
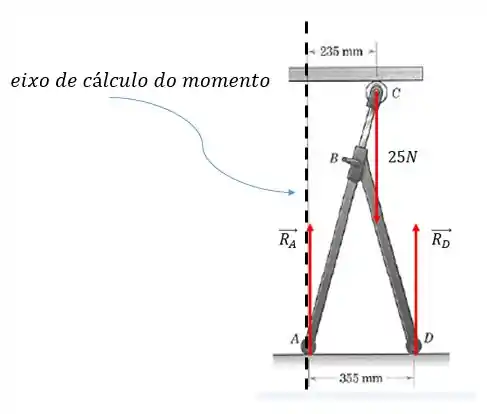
Perceba que a distância da força de até vale e a distância da força vale
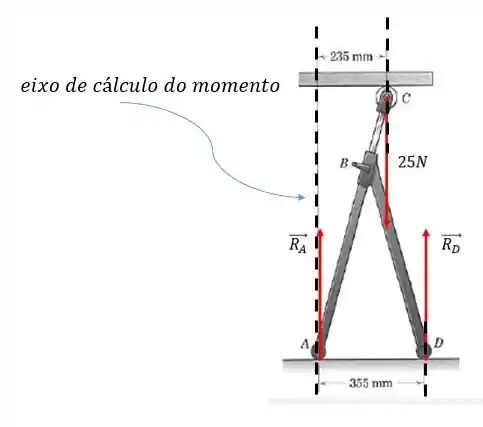
Adotando o sentido anti-horário como positivo, vamos ter que
Passo 3
Show de bola!
Agora, para achar vamos calcular momentos de novo?
Não!!! Vamos fazer uma coisa mais simples usando a outra condição:
Substituindo o valor de :