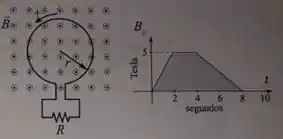
Um campo magnético uniforme é perpendicular a uma espira circular condutora de resistência desprezível, como mostrado na figura abaixo. O campo varia com o tempo como mostra a figura. (O sentido positivo do eixo é para fora da página). O raio da espira é e ela está conectada em série a um resistor de resistência .
- Qual é a expressão da induzida no circuito em função do tempo?
- Faça um gráfico da induzida em função do tempo, considerando valores e unidades. Observe os sinais. Observe o sentido positivo da deve ser consistente com a hipótese de que está saindo do papel;
- Faça um gráfico da corrente através do resistor em função do tempo, considerando valores e sinais. Indique o sentido da corrente através de para cada intervalo de tempo (horário, anti-horário ou nenhum);
- Determine a energia dissipada no resistor no intervalo de tempo entre e .
Passo 1
a) O campo magnético é uniforme, porém depende do tempo. Isso significa que, para todo instante de tempo , ele tem o mesmo valor em todos pontos da superfície plana definida pela espira. Podemos escrever o vetor campo magnético como .
Como o campo está saindo da página e é perpendicular a ela em todos os pontos, podemos colocar nosso vetor área como , ou seja, é paralelo à . Com isso, o fluxo magnético fica
Portanto, a induzida terá a seguinte expressão
Passo 2
b) Agora, vamos analisar como é o campo magnético em cada intervalo de tempo. No intervalo , olhando para o gráfico que o problema fornece, o campo magnético tem a seguinte função, que é uma reta crescente com coeficiente angular (Tesla por segundo):
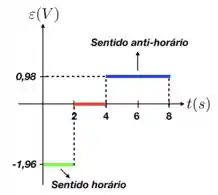
Para esse intervalo de tempo, a induzida será
que é constante e negativa.
Para o intervalo , o campo é constante e a será , já que a derivada de uma constante é igual a zero.
No intervalo , o campo magnético é reta decrescente
A induzida para esse caso será constante e igual a .
Juntando tudo isso num gráfico e lembrando que o sentido positivo é anti-horário, teremos
Passo 3
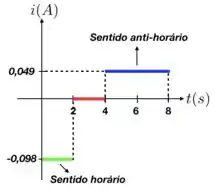
c) Como , então a corrente no primeiro intervalo do Passo 1 será igual a . Como o vetor área aponta para fora do plano da página, pela regra da mão direita, o sentido positivo para a fem e a corrente induzida será o anti-horário. Por isso, nesse primeiro intervalo de tempo, a corrente induzida estará no sentido horário.
No segundo, e no terceiro e vai circular no sentido anti-horário, sendo que este é o sentido positivo. Colocando esses valores num gráfico, teremos o seguinte
Passo 4
d) A energia dissipada será a soma das energias dissipadas em cada um dos intervalos de tempo acima. Por isso, teremos
A potência dissipada no intervalo de tempo de 10 s será
Resposta
- Ver o gráfico do Passo 2 ;
- Ver o gráfico do Passo 3 ;