Uma espira condutora retangular de superfície e resistência gira ao redor do eixo com velocidade angular constante num campo magnético uniforme de modulo B e direção e sentido ao longo do eixo como mostrado na figura ao lado.
Considere o sentido do vetor unitário característico da superfície da espira para efeito de fluxo magnético como mostrado em figura.
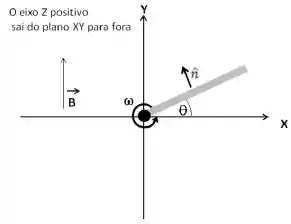
Determine o sinal do fluxo magnético que atravessa a espira e da sua derivada temporal nos seguintes intervalos:
Determine a expressão do fluxo magnético que atravessa a espira e da induzida em função do ângulo . Faça um gráfico das duas grandezas para .
Calcule a potencia elétrica dissipada no resistor em função do ângulo .
Qual deve ser a potência em função de tempo de um motor que está forçando a espira a girar com uma velocidade ? A potência média durante uma volta completa da espira é menor, maior ou igual a potencia elétrica dissipada no resistor? Justifique através de considerações energéticas.
Sugestão: A potência é igual ao momento τ aplicado pelo motor vezes a velocidade angular .
Passo 1
Determine o sinal do fluxo magnético que atravessa a espira e da sua derivada temporal nos seguintes intervalos:
O fluxo magnético, por definição, é dado por:
Onde .
Como é constante e uniforme, podemos reescrever a expressão do fluxo magnético como:
Como se trata de um produto escalar entre os vetores e , podemos dizer que:
Onde é o ângulo entre os vetores.
Assim:
Passo 2
Agora só temos que verificar o sinal de e para cada caso, beleza?
Passo 2
Determine a expressão do fluxo magnético que atravessa a espira e da induzida em função do ângulo . Faça um gráfico das duas grandezas para .
Acabamos fazendo isso no passo anterior mas, só pra constar:
O fluxo magnético, por definição, é dado por:
Onde .
Como é constante e uniforme, podemos reescrever a expressão do fluxo magnético como:
Como se trata de um produto escalar entre os vetores e , podemos dizer que:
A induzida, de acordo com a Lei de Faraday, é dada por:
Assim:
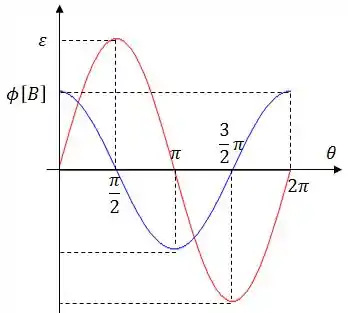
O gráfico desses caras vai ter essa cara:
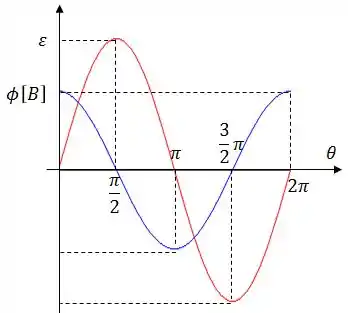
Passo 3
Calcule a potencia elétrica dissipada no resistor em função do ângulo .
Por definição, a potência elétrica no resistor é dada por:
Substituindo a expressão de que encontramos anteriormente, teremos:
Passo 4
Qual deve ser a potência em função de tempo de um motor que está forçando a espira a girar com uma velocidade ? A potência média durante uma volta completa da espira é menor, maior ou igual a potencia elétrica dissipada no resistor? Justifique através de considerações energéticas.
A potência do motor será dada por:
Então vamos começar calculando o torque magnético sobre a espira, que é dado por:
Onde . Logo:
Lembrando que , podemos reescrever a expressão acima como:
Agora, substituindo a expressão de , teremos:
Finalmente a potência do motor é dada por:
A potência do motor é igual à potência elétrica dissipada no resistor. Isso significa que o trabalho realizado pelo motor é totalmente dissipado em calor no resistor.
Resposta
A potência do motor é igual à potência elétrica dissipada no resistor. Isso significa que o trabalho realizado pelo motor é totalmente dissipado em calor no resistor.
Resposta
Ei, a resposta está no passo a passo :)