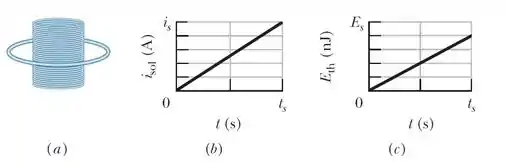
A figura abaixo mostra , em (a), uma espira circular concêntrica com um solenoide e está em um plano perpendicular ao eixo central do solenoide. A espira tem 6,00 cm de raio. O solenoide tem um raio de 2,00 cm, possui 8000 espiras/m e a corrente varia com o tempo da forma indicada na figura, em (b), onde a escala do eixo vertical é definida por e a escala do eixo horizontal é definida por . A figuramostra, em (c), em função do tempo, a energia que é transformada em energia térmica na espira; a escala do eixo vertical é definida por . Qual é a resistência da espira?
Passo 1
Bom, esse problema é um pouco complexo, devido a quantidade de informações, mas vamos com calma!
Primeiramente temos que perceber que se trata de uma questão sobre lei de Faraday. A corrente varia com o tempo e por causa diss, o fluxo do campo magnético vai variar também, e isso vai induzir uma força eletromotriz na espira.
Vamos lembrar da fórmula da lei de Faraday:
Como essa questão não pergunta nada sobre o sentido da força eletromotriz induzida, nem de sua corrente, eu vou suprimir esse sinal de menos da equação.
Mas:
Como no nosso problema a espira está posicionada em um plano perpendicular ao eixo central do solenoide:
E então:
Agora precisamos lembrar que o campo magnético no interior de um solenoide é dado pela fórmula:
Sendo que é a corrente passando pelo solenoide e é o número de espiras por unidade de comprimento.
Obs.: o campo magnético do lado de fora do solenoide é zero!
Entao ficamos com:
Vamos dar nome aos bois:
: força eletromotriz induzida;
: área do solenoide;
: permeabilidade magnética do vácuo, com valor
: corrente elétrica no solenoide;
: tempo.
Passo 2
Agora vamos avaliar o que diz a figura (b).
Na figura (b) temos que
Sendo e
Substituindo na formula:
Passo 3
Agora vamos lembrar das equações lá de circuitos com resistores envolvendo a taxa de dissipação da energia elétrica devido a uma resistência:
Temos duas:
Como nós temos o valor da força eletromotriz induzida na espira mas não temos a corrente induzida na espira, vamos utilizar a segunda fórmula:
Rearranjando:
Agora precisamos achar a potência, ou seja, uma taxa de energia por tempo.
Passo 4
Agora vamos avaliar o que diz a figura (c).
Na figura (c) temos que .
Repara que a a escala é dividida em 5 partes mas a reta só vai até a quarta parte, ou seja, da escala total de 100 nJ, que é 80 nJ. Fica ligado!
Voltamos a nossa formula: