Calcule os limites.
Passo 1
Fala aí, bora matar mais essa questão aqui no peito! A questão pede pra gente calcular o limite tendendo ao infinito e para calcular o limite de uma função vetorial precisamos calcular o limite de cada um dos seus componentes.
Sendo que o primeiro termo corresponde ao componente , o segundo termo corresponde ao componente e o terceiro termo corresponde ao componente .
Passo 2
Limite do componente :
Substituindo diretamento o limite, teremos uma indeterminação do tipo:
Então precisavos tentar resolver de outra maneira.
O melhor método pra resolver quando temos divisão de polinômios e o limite tende a intinito, é colocarmos em evidencia a variável de maior grau! No caso o .
Parece complicado o que eu disse? Acompanha comigo. Antes vamos multiplicar em cima e em baixo por :
Agora que temos o nos dois termos, tanto em cima quando embaixo, vamos colocar ele em evidência na frente dos parênteses:
Fazendo isso, consiguimos cortar os dois , e ficar com
Observa que agora, quando eu for aplicar o infinito dentro do limite eu vou ter divisões por infinito, que a gente sabe que dá zero!
Prontinho, conseguimos calcular o limite sem cair em intederminação.
Passo 3
Limite do componente :
Essa daqui pode ser um pouco chatinha, mas se você vier comigo a gente resolve. Lembra como é o gráfico de
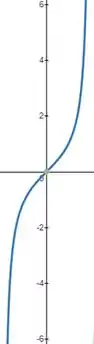
Como estamos trabalhando com a inversa dela, ou seja, , isso é como se a gente girasse ela, trocando o eixo por , ficando
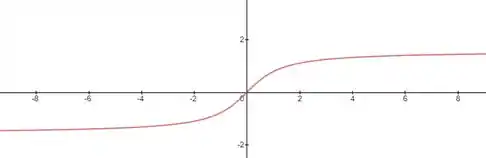
Então, como a tg fica com restrito entre , sabemos que essas vão ser as assíntotas horizontais agora!
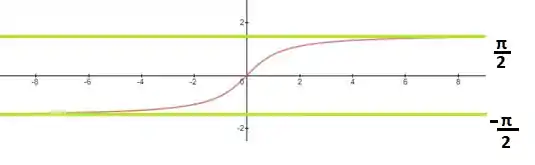
Observa então que quando o dessa nossa função está la no infinito, sabemos que vai tender pra . A nível de curiosidade a gente consegue também observar que caso o limite fosse pra menos infinito, a função iria para .
Assim a gente acabou de descobrir o limite desejado:
Passo 4
Limite do componente :
Vamos primeiramente separar essa subtração na fração, ficamos então com
Como aquele exponencial está elevado a um número negativo, podemos colocar ele no denomidador
Agora vamos simplesmente substituir o infinito na função
Um numero inteiro dividido porá infinito sabemos que dá zero, certo? Então temos:
Passo 5
Desta forma: