UNICAMP – Física 1 – 2020.2 – P3 – Exercício 3
Um bloco de inércia e um bloco de inércia são conectados por uma corda com inércia desprezível sobre uma polia em forma de um disco sólido com raio e inércia . A rampa faz um ângulo de . O coeficiente de atrito cinético é para ambos os blocos. Use .
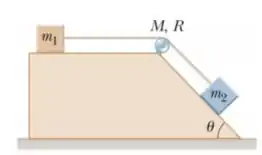
a) Desenha diagramas de corpo livre para o bloco 2 e o diagrama de corpo livre estendido para a polia.
b) Determine a aceleração dos dois blocos.
c) Calcule as tensões na corda, presa no bloco 1 e presa no bloco 2.
d) Qual a aceleração angular da polia?
Passo 1
Fala galerinha, beleza? Partiu resolver esse problema sobre bloquinhos?
O primeiro passo é desenhar as forças que agem em cada bloco:
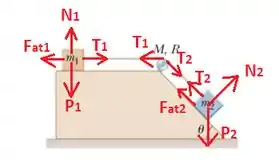
No bloco 1, temos o peso, normal, força de tração e atrito contrária ao movimento. No corpo 2, temos o peso, normal, atrito e tração. Já na polia, temos as duas trações e .
Passo 2
Vamos escrever as equações de movimento para cada corpo. No corpo 1, temos
Como , segue que
Guarde essa equação!
No corpo 2, temos que decompor o peso, de modo que
Como , segue que
Agora vem um ponto importante: considerando o fio inextensível, devemos ter , de modo que
Vamos substituir todos os valores:
Logo,
Repare que temos um problema: são duas equações para três incógnitas. Como resolver esse problema?
Passo 3
Temos que olhar para a polia! O torque sobre ela é
Por outro lado, a segunda lei de Newton para rotação nos diz que
Logo,
O momento de inércia do disco é
Já a aceleração angular se relaciona com a linear por
Desta forma,
Essa era a equação que faltava:
Logo,
Somando as três equações:
Passo 4
Para achar as trações, é só voltar no sistema:
Com isso,
Já para encontrar a aceleração angular da polia, basta fazer
Portanto,
Com isso a gente termina o problema 😊!