Um bloco de massa está pendurado por um fio ideal que está enrolado em uma polia fixa, mas que pode girar em torno de um eixo que passa pelo seu centro e é perpendicular ao plano da polia. À medida que o bloco desce, o fio vai se desenrolando e a polia vai adquirindo uma velocidade de rotação cada vez maior, como sugere a figura abaixo. Suponha que o fio não deslize sobre a periferia da polia. A polia tem raio e observa-se que o bloco desce com aceleração constante de módulo . As respostas devem ser dadas em termos dos dados do problema: , , e da aceleração da gravidade .
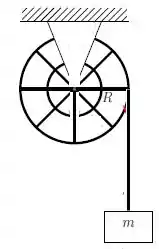
a) Supondo que o sistema parte do repouso, quanto tempo leva para que a polia dê a primeira volta completa em torno do eixo de rotação.
b) Faça um diagrama das forças que atuam sobre o bloco e sobre a polia.
c) Qual o momento de inércia da polia em relação ao seu eixo de rotação?
Passo 1
Basicamente, o bloco está sendo puxado para baixo pela força peso e acaba fazendo a polia girar a partir do cabo que está enrolado nela.
Primeiro de tudo, como não há deslizamento entre o cabo e a polia, a aceleração do cabo é a mesma que a aceleração tangencial da polia.
Podemos relacionar isso com a aceleração angular :
Passo 2
Agora que já sabemos a aceleração angular da polia , podemos encontrar o tempo necessário para que ela dê uma volta.
Como essa aceleração é constante, temos um movimento circular uniformemente acelerado...
Ou seja, podemos aplicar a equação do deslocamento.
Para lembrar, podemos fazer um paralelo com a translação:
Olha bem como é parecida:
Passo 3
Qual é o deslocamento angular de uma volta?
Bom uma volta é igual a , que corresponde a em radianos:
Aplicando na equação, a polia parte do repouso, logo:
Passo 4
Queremos tudo em função dos dados do problema, então vamos usar a relação que achamos para no PASSO 1:
Assim:
Achamos que o tempo para a polia completar uma volta completa é:
Passo 5
Na letra (b), queremos um diagrama de forças sobre o bloco e sobre a polia.
Vamos começar com o bloco:
Temos uma força peso para baixo e uma força de tração para cima:
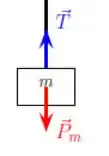
Agora, vamos à polia:
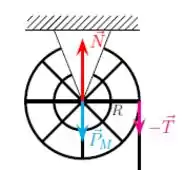
Como a polia é não-ideal, ela apresenta uma massa e portanto uma força peso para baixo.
Além disso existe também uma força de tração por meio da corda.
Para equilibrar essas duas forças, deve existir uma força normal para cima no suporte:
Passo 6
Na letra (c), queremos o momento de inércia da polia.
Muito cuidado...
Não queremos aquela fórmula pronta de momento de inércia para um disco.
Queremos em função dos dados do problema (, , e ).
Então, vamos encontrá-lo de outra forma.
Vamos aplicar a segunda lei de newton para rotação:
Já sabemos que a aceleração angular é:
Resta saber quem é o torque resultante.
Passo 7
Olhando de novo para a polia, o torque resultante será a soma de todos os torques:
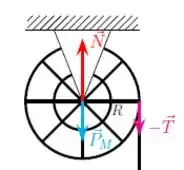
Porém, tanto a força peso quanto a força normal estão aplicadas no centro de rotação da polia, logo, seus torques são nulos:
Enquanto isso, a força de tração atua tangencial à polia.
Logo, seu torque será:
Assim, a segunda lei fica:
Mas repara que não conhecemos a força de tração ...
Passo 8
Para achar a força de tração, devemos aplicar a segunda lei de Newton para o bloquinho:
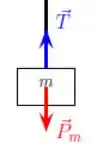
O bloco apresenta uma aceleração para baixo, então:
Agora sim, temos a força de tração em função dos dados do problema.
Passo 9
Substituindo o na expressão dos torques:
Aplicando também a relação de :
Assim, temos que o momento de inércia é:
Resposta
(a)
(b)
Bloco:
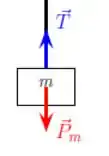
Polia:
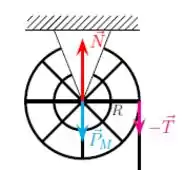
(c)