Na figura, um fio sem massa e inextensível passa sem escorregar ao redor da polia. Numa extremidade do fio é pendurado um bloco de massa m2 = 500 g, na outra, um bloco de massa m1 = 400 g, e a polia, que é um disco homogêneo montado num eixo horizontal sem atrito, tem um raio de 5,00 cm. Quando o sistema é abandonado a partir do repouso, o bloco de massa maior cai 75,0 cm e adquire uma velocidade linear de 30,0 cm/s.
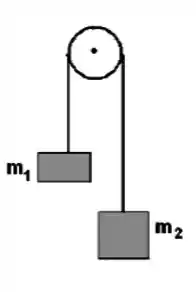
a) Faça os diagramas de força para cada bloco e polia.
b) Utilizando a conservação de energia mecânica determine a inércia rotacional da polia.
c) Determine o módulo e sentido da aceleração angular da polia.
d) Determine as tensões no fio e o vetor reação do eixo de rotação sobre a polia.
e) Qual é o vetor torque resultante em torno do eixo de rotação ? Faça dois cálculos, um utilizando a equação e outro .
f) Qual a força de atrito entre a corda e a polia?
Passo 1
Bom, questão de polia não-ideal!!

Vamos começar pela letra a), que é fazer o diagrama do corpo livre para os corpos dos sistema. Vai ficar assim para os blocos:
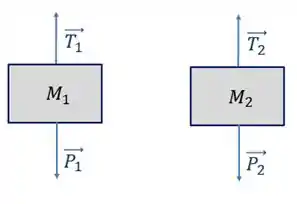
Repara que como a polia não é ideal, teremos trações diferentes para cada bloco. O DCL da polia vai ficar assim:
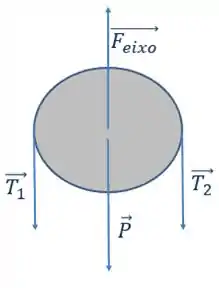
A força no eixo, é a força que o eixo da polia realiza para que ela não caia. Afinal a polia ela vai apenas rotacionar ao redor do eixo, dessa forma é necessário uma força de reação sobre o eixo.
Passo 2
A letra b), nos pede para encontrar qual é a inércia da polia e para fazer isso através da conservação de energia. Bom, vamos então montar um desenho com antes e depois do movimento para depois conservamos a energia mecânica.
Antes dos blocos se moverem, quando o sistema é solto a partir do repouso, temos a seguinte configuração:
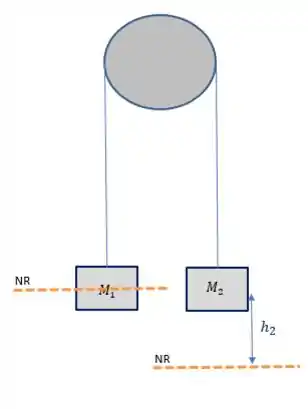
Você pode escolher qualquer nível de referência para os blocos. E eles não precisam ser os mesmos para os dois blocos, mas precisam ser os mesmo entre o início e fim!!
Eu escolhi os níveis de referência sempre na posição mais baixa que o bloco irá atingir. Agora, olhando para o final do movimento, teremos:
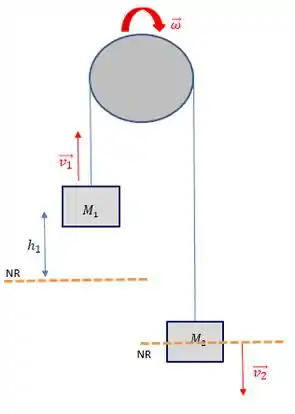
Vamos então conservar a energia mecânica.
Daonde sabemos que e são a distância que os blocos percorreram, que é a mesma e vale 75cm.
Além disso, as velocidades dos blocos é a mesma, afinal eles fazem parte do mesmo sistema.
E olhando para a velocidade angular da polia, podemos relaciona-la com a velocidade em sua extremidade, que é a mesma velocidade que os blocos pela relação:
Substituindo tudo, teremos:
Passo 3
Agora, na letra c), nos pede para encontrar o módulo e a direção da aceleração angular da polia. Chegou a hora de olhar para as forças nesse sistema, e resolver as segundas leis de newton.
Lembra os diagramas do corpo livre que a gente fez, vamos reutiliza-los, mas indicando a direção da aceleração.
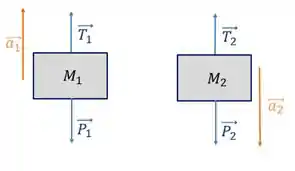
Considerando o sentido da aceleração de cada bloco como o sentido positivo para as suas forças, podemos calcular a segunda lei de newton para cada um deles.
Aaaa, não vamos esquecer que esses blocos pertencem a um sistema preso por uma corda, e eles se movimentam juntos, logo
Agora para finalizar, vamos ver o DCL da polia:
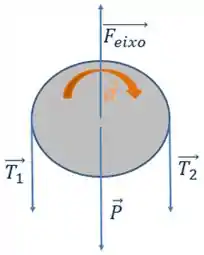
Para a polia, nós faremos a segunda lei de newton para a rotação (afinal, ela só vai rotacionar né). Para isso vamos avaliar os torques em relação ao eixo de rotação e os torques na direção da aceleração angular serão positivos.
Substituindo os valores das trações que encontramos, vai ficar:
Agora, é só lembrar que a aceleração angular da polia tem relação com a aceleração na sua extremidade (que é igual a aceleração dos blocos).
Substituindo, vai ficar assim.
O sentido da aceleração já tá indicado no desenho com o diagrama do corpo livre da polia.
Passo 4
A letra d), nos pede o valor das tensões no fio e o valor da força de reação sobre o eixo da polia. Para encontrar as tensões é só substituir o valor da aceleração angular nas fórmulas que encontramos no passo 3.
Agora, para encontrar o valor da força de reação sobre o eixo da polia, nós iremos olhar para o DCL da polia lembrando que a polia apenas rotaciona, não translada. Por tanto, sua aceleração é 0 e com isso a força resultante também é:
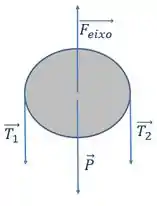
Precisamos encontrar o valor do peso da polia. Para isso, precisamos saber a sua massa.
Uma polia é um disco que rotacional ao redor do eixo que passa pelo seu centro de massa. O momento de inércia de um disco é tabelado e dado por:
Assim, conseguimos encontrar a sua massa:
Com isso, encontramos a força de reação sobre o eixo como sendo:
Passo 5
A letra e) pede para encontrar o torque resultante sobre o eixo da polia. Primeiro através de .
Como a força é perpendicular ao raio, o módulo do torque resultante será dado por:
E depois através de .
Os dois valores deveriam ser iguais. A pequena variação nos valores ocorreu por conta de aproximações.
Passo 6
A letra f) pergunta sobre a força de atrito entre a corda e a polia.Na questão nos diz que a polia não tem atrito com o eixo. E isso ocorre para que não haja um torque contrário ao torque causado pelas trações.
Agora, entre a corda e a polia, a força de atrito entre eles, é a própria força de tração que faz com que a polia rotacione. Pensa comigo, se você coloca óleo em uma polia, a corda desliza sobre ela, né. Isso acontece por que você está tirando o atrito entre a corda e a polia e assim a polia não "sente” a tração da corda.
Resposta
b)
c)
Sentido entrando na página (horário).
d)
e)