Os blocos de massas e estão conectados por uma corda sem massa que passa por uma polia, como mostrado na figura. A polia é um disco homogêneo que pode girar em torno do seu eixo sem atrito. A massa desliza sem atrito sobre uma superfície horizontal. Os dois blocos estão em repouso quando a massa é liberada.
a) suponha que a massa da polia seja desprezível. Encontre as acelerações dos blocos e e a tensão na corda.
b) Suponha agora que a massa da polia é e seu raio é R. Encontre a aceleração de e as tensões nas partes vertical e horizontal da corda. Verifique que seus resultados condizem com os obtidos no item a) quando você faz =0
Passo 1
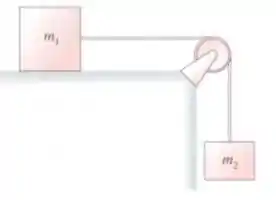
Na letra a), a massa da polia é considerada como desprezível, ou seja, temos uma polia ideal. Então, o que faremos aqui, é o que já fazíamos nos capítulos anteriores. Vamos fazer o famoso DCL dos dois blocos e resolver a questão por segunda lei de newton.
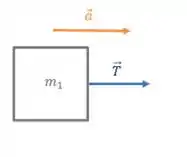
Daonde teremos pela segunda lei:
Já para o segundo bloco teremos:
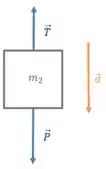
E pela segunda lei:
Os dois blocos possuirão a mesma aceleração () pois estão ligados por uma corda inextensível, e a tração nos dois blocos é a mesma, pois a polia é ideal.
Substituindo a tração da primeira equação na segunda teremos:
Daonde encontramos a aceleração dos blocos:
Substituindo essa aceleração na primeira equação teremos:
Passo 2
Na letra b), a parada complica um bocado, pois agora a polia possui massa e ela não é mais ideal. Agora que ela possui massa, precisaremos fazer o DCL também para a polia!!
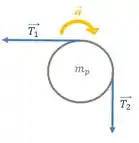
A primeira diferença gritante que encontramos aqui é que as trações não são mais as mesmas. Pois como precisamos de um torque resultante, é necessário que seja diferente de .
A polia é um corpo que está livre para rodar, por isso, iremos realizar a segunda lei de Newton para a rotação nela, que é:
O momento de inércia da polia é o mesmo momento de inércia para um disco homogêneo em relação a um eixo que passa pelo seu centro de massa, que é tabelado:
Analisando o torque gerado por cada tração e levando em consideração a direção do torque (vamos considerar a direção da aceleração angular como positiva, ou seja, a direção horária), teremos:
Passo 3
Agora, faremos o DCL e a segunda lei para cada um dos blocos:
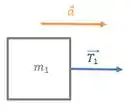
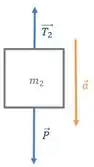
Passo 4
Agora, a grande sacada para resolver questão de polia não ideal é saber relacionar a aceleração angular com a aceleração linear, repara só:
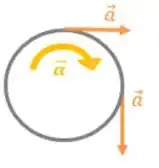
Podemos encontrar a aceleração linear de um ponto de um corpo, sabendo a aceleração angular dele e a distância do ponto com o eixo de rotação, pela fórmula:
Ou
E repara que essa aceleração, que está desenhada no corpo acima, é a mesma aceleração do bloco da horizontal e também a mesma aceleração do bloco da vertical.
Substituindo na equação da segunda lei para a polia teremos:
Ficamos assim com as seguintes equações:
Passo 5
Agora é só brincar com essas 3 equações para encontrarmos os valores.
Substituindo as trações das equações 2 e 3 na equação 1, teremos:
Deixando em evidência:
Agora dando uma ajeitada nessa fração, eu vou multiplicar em cima e embaixo por :
As trações podem ser encontradas ao substituir essa aceleração lá nas equações 2 e 3:
Passo 6
Finalmente, o último passo dessa questão é verificar se esses resultados batem com os resultados encontrados lá no PASSO 1, quando a polia não tinha massa.
A aceleração encontrada no PASSO 5, sem considerar a massa da polia fica:
Que é o mesmo valor encontrado no PASSO 1.
A duas trações também precisam ser iguais ao valor da tração encontrada lá no início:
Vemos aí, que se for zero as duas trações são iguais e batem com o valor encontrado lá no PASSO 1.
Resposta
a)
b)