O objeto ilustrado ao lado é composto por um cilindro de raio , uma haste rígida e dois discos afastados do eixo de rotação. O objeto tem momento de inércia . Ao longo do perímetro do cilindro está enrolada uma corda inextensível de massa desprezível. Outra parte desta corda está enrolada em uma roldana de raio e momento de inércia . Na extremidade da corda está uma pequeno cubo de massa , distante de um suporte. Não há deslizamento na corda. Inicialmente o sistema é mantido em repouso através de um freio. No instante o freio é retirado e o sistema inicia seu movimento. Utilize para a aceleração da gravidade.
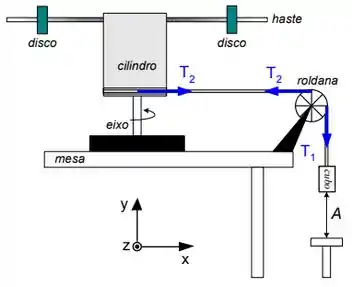
b) Determine a razão entre os módulos das acelerações angulares da roldana e do objeto .
c) Determine o módulo da aceleração linear com que o cubo cai em função dos parâmetros dados.
Passo 1
Quando o freio é retirado, o bloquinho começa a descer devido à ação da gravidade.
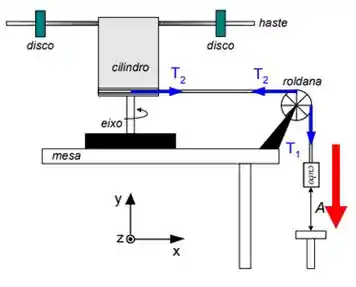
E consequentemente, ele puxa a corda que faz a roldana e aquele objeto estranho entrarem em rotação.
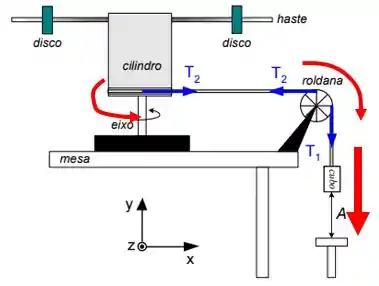
Deu pra entender melhor?
Passo 2
Na letra (b), queremos a razão entre as acelerações angulares da roldana e do objeto.
O que está conectando a roldana ao objeto?
É a corda enrolada na extremidade de cada um deles, né.
Bom, a corda tem uma mesma aceleração linear . Ou seja, tanto a roldana quanto o objeto apresentam a mesma aceleração tangencial .
Podemos ainda relacionar a aceleração tangencial com a aceleração angular de cada um deles a partir de:
Onde será o raio de cada um deles.
Então, temos:
Igualando os dois:
Passo 3
Na letra (c), queremos a aceleração linear do cubo.
Para isso, vamos aplicar a Segunda Lei de Newton nos três corpos que estão entrando em movimento de translação ou rotação (bloquinho, roldana e objeto).
Para o bloquinho, temos a força peso e força de tração atuando sobre ele:

Passo 4
Sobre a roldana, temos as duas forças de tração:
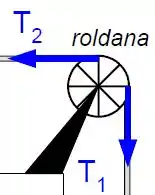
Vamos aplicar a segunda lei de Newton para rotação:
O momento de inércia da roldana é :
E quem é o torque resultante sobre a roldana ?
Passo 5
O torque é dado pelo produto vetorial entre o vetor posição e o vetor força :
Como esses vetores são perpendiculares, o módulo do torque é dado por:
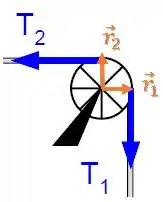
Considerando o sentido horário positivo (sentido da aceleração da roldana), o torque resultante será:
O raio da roldana é :
Passo 6
Para o objeto, a situação é parecida.
Como o momento de inércia do objeto é , a segunda lei de Newton para rotação fica:
Olhando ele por cima, vemos:
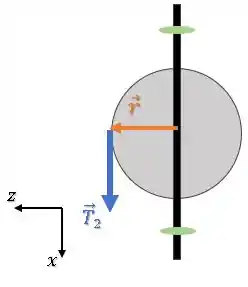
O raio do objeto é , então o torque resultante fica:
Passo 7
Ficamos com esse sisteminha aqui:
Como queremos achar a aceleração do bloco , vamos substituir as acelerações angulares através da relação do item (b).
Para a roldana:
Para o objeto:
Substituindo isso no nosso sistema:
Agora, vamos trabalhar as equações para encontrar .
Vamos passar o e o para o lado direito das equações.
Passo 8
Substituindo a terceira equação na segunda, temos:
Substituindo o valor de na primeira equação:
Resposta
(b)
(c)