(as respostas para este item devem ser dadas com casas decimais e em notação científica) Um tubo sonoro com duas extremidades abertas de comprimento que ressoa no modo (A velocidade do som no ar está dada na capa da prova).
- Faça um desenho no tubo abaixo representando a onda sonora se propagando no tubo com duas extremidades abertas para . Identifique a posição e escreva os valores dos nós e dos anti-nós tomando por referência a extremidade esquerda como posição e a extremidade direita como posição
- Determine a frequência emitida pelo tubo
- Determine o comprimento de onda da onda emitida pelo tubo
- Um segundo tubo com um tamanho ligeiramente menor que o primeiro também com a extremidade aberta é colocado próximo ao tubo descrito anteriormente. Quando passa ar por estes dois tubos, é ouvido um batimento com frequência de . Qual o comprimento deste segundo tubo
Passo 1
Fala povo, tudo ok? Vamos lá! Pra início de conversa, vamos lembrar que em tubos abertos, o número de harmônicos é o número de metades de comprimentos de onda que nós temos. Ou seja, se entendermos esse desenho:
Como dois quartos, ou seja, uma metade de um harmônico, nosso esboço dentro de
Tem que caber vezes o primeiro desenho. Ficamos então com:
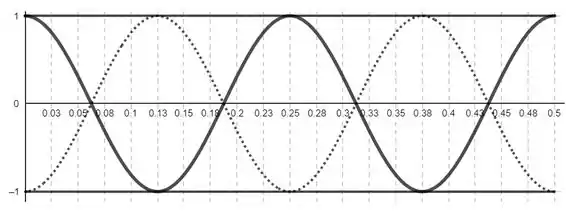
Show, agora é hora da gente lembrar o seguinte: quando falamos de nós, queremos os valores em que as duas ondas na figura do enunciado se encontram. E quando falamos de anti-nós, queremos os pontos onde a amplitude é máxima! Combinado? Pra pegar os nós, podemos fazer a média dos números exibidos na imagem. Por exemplo, o primeiro nó ta no meio do caminho entre e . Ou seja, ele está em algo perto de:
Portanto, podemos resumir nossos nós, seguindo essa lógica, para:
![]()
Já os antinós, basta olhar pros pontos que acabam tocando . Bora então! Vamos ter:
![]()
Passo 2
Ok galera, fim da letra , partiu ir pras próximas letras!! A questão não falou que estamos no quarto harmônico? Então se cabem quatro metades de comprimento de onda dentro do tubo, podemos relacionar e da seguinte forma:
O valor de que é o comprimento do tubo, nós temos. Então o comprimento de onda vai ser:
Agora, na letra , a questão quer que a gente ache o comprimento da onda emitida pelo tubo. De forma geral galera, sempre ta certo considerar, pra ondas:
Como a onda emitida pelo tubo se propaga na velocidade do som, que é dada como sendo , temos a seguinte frequência de emissão:
Então a letra e tão respondidas! Vamos ter:
Passo 3
Pra fechar com chave de ouro, vamos pra uma outra questão. O pulo do gato é a gente entender que se um outro tubo menor está próximo desses, é possível relacionar as frequências da seguinte forma:
Onde é a frequência do novo tubo e do primeiro. Note que, como o tubo é menor, sua frequência deverá ser maior! Oras gente, temos todos os dados pra achar . Seja, do enunciado, :
Ok ok, mas como eu acho o comprimento do tubo com isso? Calma gafanhoto, se usarmos essa fórmula aqui:
Tudo sai tranquilo! Afinal:
Sendo porque estamos falando do quarto harmônico, a velocidade do som no ar e a frequência o que acabamos de achar, temos:
Não é que o tubo é ligeiramente menor mesmo?? Fechamos essa questão!
