Ondas Sonoras
- Um tubo de comprimento é fechado em uma extremidade Um fio de aço, de de comprimento e massa de , é esticado e colocado pra oscilar próximo à extremidade aberta do tubo. O fio, fixo nas duas extremidades, vibra numa frequência correspondente ao segundo harmônico. Essa vibração produz na coluna de ar dentro do tubo uma oscilação que corresponde ao primeiro harmônico. Considere a velocidade do som como
- Encontre a frequência de oscilação da coluna de ar.
- Desenha o tubo e faça uma representação transversal(tipo corda) dos nós e antinós de pressão para essa frequência.
- Calcule a tensão no fio
- Você está parado a uma distância de uma fonte pontual que emite ondas sonoras de forma isotrópica(igualmente em todas as direções). Ao caminhar em direção à fonte, observa que a intensidade foi dobrada.
- Calcule a distância
- Encontre a frequência de oscilação da coluna de ar.
- Desenha o tubo e faça uma representação transversal(tipo corda) dos nós e antinós de pressão para essa frequência.
- Calcule a tensão no fio
- Você está parado a uma distância de uma fonte pontual que emite ondas sonoras de forma isotrópica(igualmente em todas as direções). Ao caminhar em direção à fonte, observa que a intensidade foi dobrada.
Passo 1
a):
Entendendo esse problema: Existem duas fontes de frequência: O tubo de ar e o fio.
Ambos vibram com a mesma frequência, mas, enquanto essa frequência é o segundo harmônico do fio, é o primeiro harmônico do tubo de ar.
Mas aqui queremos saber a frequência do tubo de ar( que será a mesma do fio).
Então vamos usar a fórmula das frequências pra tubos fechados:
O primeiro harmônico ocorre pra
Passo 2
b):
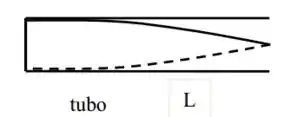A extremidade fechada de um tubo é um nó pro deslocamento e por isso é um ventre pra pressão ( antinó).
Já a extremidade aberta é um nó pra pressão, já que está em contato com a pressão atmosférica e essa não oscila, e, portanto, é um antinó (ventre) pro deslocamento.
Passo 3
c):
Aqui a gente vai ter que fazer umas mágicas.
Bom, como a frequência é a mesma pros dois corpos, vamos usar isso pra descobrir a velocidade de propagação das ondas estacionárias no fio:
E :
Então:
Então, usando a equação abaixo:
Vamos calcular :
Então:
Passo 4
d):
Dizer que a fonte de ondas emite de forma isotrópica é o mesmo que dizer que podemos usar a equação abaixo:
Vamos chamar
O que o enunciado diz é que gera o dobro da intensidade, isso é, . Então:
Substituindo o valor de
Resposta
a):
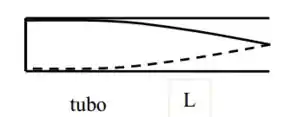
b):
c):
d):