4 - Uma corda de guitarra possui atualmente uma frequência fundamental de . Que porcentagem de aumento de tensão é necessária se quisermos reajustar essa frequência fundamental para ?
Passo 1
Poxa, sabemos que a velocidade de uma onda na corda de uma guitarra (corda presa) pode ser dedos em termos da tensão que os seus dedos exercem nela assim:
Onde é a tensão e é a densidade de massa linear da corda.
Velocidade está ligada a frequência por:
Onde é o comprimento de onda da frequência.
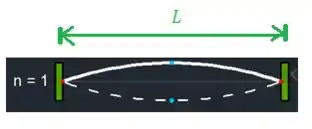
Ora bolas, sabemos que a guitarra possui as cordas presas nas duas extremidades, de forma que o primeiro harmônico seja assim:

Poxa, para ter um comprimento de onda são necessários dois gomos desses, afinal essa é a definição de :
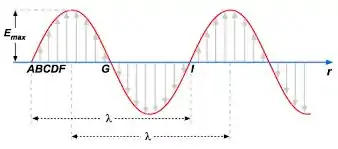
Então, no nosso caso, sendo o comprimento da corda do violão...
Concluímos que a frequência pode ser dada por...
Passo 2
Show! A frequência atual é e a frequência que queremos é . Então, chamando o atual de e o que queremos de ...
Veja que não muda (porque é duas vezes o comprimento da corda), e nem (densidade que só depende de como a corda foi construída). As únicas coisas que mudam são as frequências e as tensões. A divisão do que queremos por o que a gente já tem simplifica as coisas...
Como pela divisão de raízes podemos jogar tudo dentro de uma única raiz...
Substituindo as frequências...
Isso significa que é ou maior que .
Resposta
Letra B.