A área da região no primeiro quadrante limitada pela parábola e pela reta é de unidades quadradas. Encontre o centróide.
Passo 1
Para encontrar o centróide, vamos usar as relações:
Mas, por sorte, o enunciado já nos dá a área da região, então não precisamos calcular a integral do denominador, já que:
Então só vamos precisar calcular as integrais dos numeradores para encontrarmos nosso centróide. Vamos ver como que fica!
Passo 2
Vamos começar tentando entender melhor nossa região, já que vamos precisar descrevê-la para calcularmos nossa integral dupla.
Se esboçarmos a parábola e a reta , vamos ter algo do tipo:
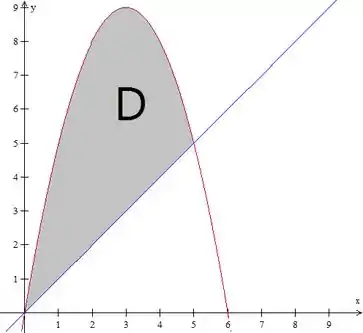
Temos uma região do tipo , com variando entre e aquele ponto de interseção, que se dá em:
Então nossa região vai ser descrita por:
E agora podemos calcular nossas integrais.
Passo 3
Vamos começar pela de , lembrando a fórmula:
Então,temos que calcular:
Mas como temos nossa região descrita já, podemos fazer:
Agora, se substituirmos na fórmula lá de cima, vamos ter:
Passo 4
Agora vamos fazer a mesma coisa para :
Então vamos calcular:
Que se substituirmos na fórmula, vai nos dar: