Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Centroide de Regiões Planas

Ver Teoria
Exercício 81234567910111213141516171819202122232425

Enunciado

  1. Calcule o centro de massa do conjunto D = x ,   y ; 1 ≤ x 2 + y 2 ≤ 4 ,   y ≥ 0 , sendo a densidade proporcional à distância do ponto à origem.

Passo 1

Então, a primeira coisa a se fazer em exercícios como esse é esboçar a sua região. Vamos lá?

Bem, primeiramente, a região D é formada pelas inequações 1 ≤ x 2 + y 2 ≤ 4 . Mas... Se ao invés de pegarmos as inequações, olhássemos para as equações a partir dela

x 2 + y 2 = 1

x 2 + y 2 = 4

RARA! Essa equações nos representa circunferências de raio 1 e a outra de raio 2 . Ambas centradas na origem.

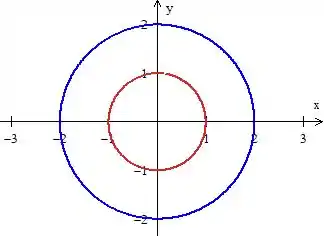
Mas o problema também nos delimita apenas na parte de cima, onde y ≥ 0 . Assim, a região D é

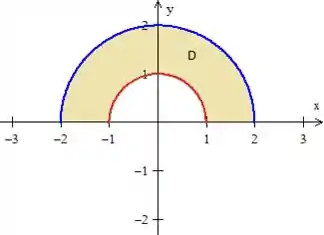
Passo 2

Muito bem! Para calcular a o centro de massa dessa coisa, devemos calcular antes três integrais extremamente importantes:

1 )     ∬ D y     ρ x ,   y d A

2 )     ∬ D x     ρ x ,   y d A

3 )     ∬ D ρ x ,   y d A

Agora, repare que em ambas devemos saber quem é essa função densidade ρ x ,   y , o que é muito fácil encontrar, afinal de conta ela é proporcional à distância d à origem. Como a essa distancie é

d = x 2 + y 2

então

ρ x ,   y = k x 2 + y 2

k é a constante que indica proporcionalidade, ok?

Bem, mas não é só a função de densidade que devemos conhecer...

Passo 3

Precisamos saber também a respeito desse sólido D aí!

Ora! Já conhecemos quem é o sólido, mas precisamos descrevê-lo para podermos trabalhar.

Como estamos trabalhando com um pedaço de círculo... Podemos pensar em uma mudança para as coordenadas polares

x = r cos ⁡ θ

y = r sin ⁡ θ

O Jacobiano desse tipo de mudança é

J = r

e uma equação que nos ajuda, tipo, muuuuito é

x 2 + y 2 = r 2

sacou?

Passo 4

Agora se lembre, não podemos terminar uma mudança sem antes sabermos onde estão variando os novos caras, no caso, r e θ :

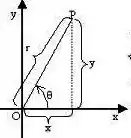
Por comparação com...

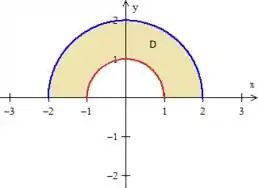
podemos ver que θ dá uma meia volta começando de 0 ° e indo até 180 °

0 ≤ θ ≤ π

enquanto que o r varia da circunferência menor vermelha indo até a curva azul

c u r v a   v e r m e l h a ≤ r ≤ c u r v a   a z u l

1 ≤ r ≤ 2

Passo 5

Retornando a primeira integral que devemos resolver...

1 )     ∬ D y     ρ x ,   y d A = ∬ D y     k x 2 + y 2 d A

e substituindo...

∫ 0 π ∫ 1 2 r sin ⁡ θ ∙ k r ∙ J   d r d θ =

k ∫ 0 π ∫ 1 2 r 3 sin ⁡ θ   d r d θ

integrando separadamente r , esse seno...

∫ 0 π sin ⁡ θ ∫ 1 2 r 3   d r d θ

∫ 0 π sin ⁡ θ r 4 4 1 2 d θ =

2 4 4 - 1 4 ∫ 0 π sin ⁡ θ d θ =

e resolvendo a integral de for obteremos...

15 4 - cos ⁡ θ 0 π = 15 4 - cos ⁡ π - - cos ⁡ 0

= 15 2

Passo 6

Quanto à outra integral...

2 )     ∬ D x     ρ x ,   y d A = ∬ D x     k x 2 + y 2 d A

Repetindo o processo

k ∫ 0 π ∫ 1 2 r cos ⁡ θ r ∙ r   d r d θ =

∫ 0 π ∫ 1 2 r 3 cos ⁡ θ d r d θ

resolvendo a integral de dentro

∫ 0 π cos ⁡ θ ∫ 1 2 r 3 d r d θ =

k ∫ 0 π cos ⁡ θ r 4 4 1 2 d θ =

k 2 4 4 - 1 4 ∫ 0 π cos ⁡ θ d θ =

Para essa integral

2 4 4 - 1 4 - sin ⁡ θ 0 π =

2 4 4 - 1 4 - sin ⁡ π - - sin ⁡ 0 = 0

Passo 7

Calma! Não se estressa! Mas temos mais uma integral a se resolver...

∬ D ρ x ,   y d A = ∬ D   k x 2 + y 2 d A

Basta substituir e resolver tuuuudo novamente como segue

∫ 0 π ∫ 1 2 k r ∙ r   d r d θ =

resolvendo primeiro a integral de dentro...

∫ 0 π ∫ 1 2 r 2   d r d θ =

∫ 0 π r 3 3 1 2 d θ =

2 3 3 - 1 3 π = 7 3 π

Passo 8

Agora basta substituir nas fórmulas do centro de massa, ou seja:

x - = ∬ D x     ρ x ,   y d A ∬ D ρ x ,   y d A

y - = ∬ D y     ρ x ,   y d A ∬ D ρ x ,   y d A

onde vamos obter

x - = 0 7 π 3 = 0

y - = 15 2 7 π 3 = 4 5 14 π

Resposta

0 ,   4 5 14 π

Exercícios de Livros Relacionados

(a) Verifique que f x ,y = 4 x y , s e0 ≤ x ≤ 1,0 ≤ y ≤ 1 0 , c a s oc o n t r á r i o á é uma função densidade conjunta.(b) Se X e Y são variáveis aleatórias cuja função densidade conjunta é f da par
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é uma região triangular com vértices 0 ,0 ,2 ,1 ,0 ,3 ; ρ x ,y = x + y
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento a , se a densidade em qualquer ponto for proporcional ao quadrado da sua distâ
Xavier e Yolanda têm aulas que terminam ao meio-dia e concordaram em se encontrar todo dia depois das aulas. Eles chegam em um café separadamente. O tempo de chegada de Xavier é X e o da Yolanda é Y ,
Encontre o centro de massa da lâmina do Exercício 13 se a densidade em qualquer ponto for inversamente proporcional à sua distância da origem.