Determine a massa e o centro de massa da lâmina que ocupa a região e tem densidade , nos seguintes casos:
b) é o triângulo de vértices , , e
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a massa e o centro de massa da região , que tem uma densidade . E existem algumas definições que nos permitem fazer isso. Assim, a gente pode calcular a massa da região usando a equação:
Onde nossos intervalos de integração são dados pelos intervalos indicados em , pra e . Além disso, podemos encontrar as coordenadas do centro de massa uma lâmina ocupando a região , por meio das equações:
Então, vamos montar nossas integrais e calcular as propriedades pedidas. Vamos lá!
Passo 2
O enunciado nos disse que nossa região varia no triângulo de vértices , , , esse aqui:
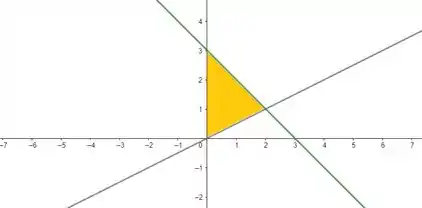
Repara que o vai de a no triângulo. E o varia da reta de baixo até a reta de cima. Como bastam apenas dois pontos pra descobrir a equação de uma reta e nós temos três pontos, fica fácil substituir os valores de e e encontrar os sistemas:
Pra reta de baixo:
Assim,
E pra reta de cima:
De modo que:
Passo 3
Então, nossa integral para a massa vai ser:
Integrando em relação , vamos ter:
Aplicando os limites de integração em :
Agora integrando em relação a :
E aplicando os limites de integração em , encontramos nossa massa:
Passo 4
Agora vamos encontrar as coordenadas do centro de massa usando as integrais do passo . Nossa primeira coordenadas é dada por:
Substituindo , que encontramos no passo anterior, e os intervalos de integração da região , temos:
Assim, integrando em relação a :
E aplicando os intervalos de integração em :
Agora integrando em relação a :
Passo 5
Agora calculando a segunda coordenada, vamos usar a equação:
Substituindo os dados da densidade, da massa e da região :
Assim, integrando em relação a e aplicando os intervalos:
E integrando em relação a :
Então, nosso centro de massa tem coordenas .
Valeu, galera! Até a próxima! 😉