Encontre o centróide da região dentro da cardióide .
Passo 1
A gente sabe calcular o centróide usando as relações:
Mas a região que nos foi dada está e coordenadas polares que, para nos lembrarmos, são:
Então, ná verdade, o que vamos calcular vai ser:
Então vamos tentar entender a região pra conseguir descrevê-la, que é só o que falta pra calcularmos as integrais!
Passo 2
Quando temos uma curva dessas complicadas com coordenadas polares, eu gosto sempre de tentar marcar uns pontos importantes pra tentar esboçar a curva mais ou menos, então vamos ver:
A curva começa com .
Para decresce de até , então decresce de até .
Para cresce em módulo de até , mas é negativo, então decresce de até .
Para decresce em módulo de até , mas é negativo, então cresce de até .
Para volta a ser positivo e cresce de até , então cresce de até , fechando a curva.
Acho que assim já da pra ter uma boa noção de como fica a curva, mas se você quiser ver como que fica ela certinha, vamos ter algo assim:
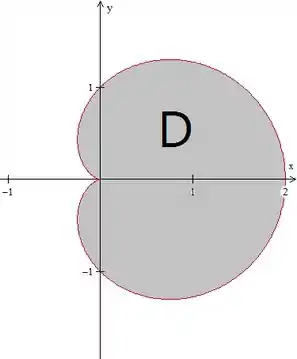
E a região vai ser descrita por:
Então agora sim podemos calcular tudo! Vamos começar com a integral do denominador que aparece nos dois termos, que é a mais simples.
Passo 3
Vamos ter:
Que, em coordenadas polares, vamos lembrar que:
Então:
Agora só falta as integrais dos numeradores, vamos ver como que é!
Passo 4
Vamos começar por :
Então vamos calcular a integral:
Que já temos a região descrita e tudo mais, então:
Eita, que contas chatas... Vamos ver cada uma separado pra não ficarmos muito perdidos.
Passo 5
A primeira:
Passo 6
Depois:
Passo 7
Mais uma:
Que fazendo pela substituição:
Passo 8
E por último:
Ufa, quanta coisa... Mas vamos ver como que fica a soma toda.
Passo 9
Somando todas aqueles nossos resultados:
Então, vamos ter que nossa coordenada vai ser:
Vamos lembrar que , então:
Agora só falta a coordenada e, sinceramente, eu espero que seja bem mais fácil, que essa foi um saco, né? Mas vamos ver!
Passo 10
Vamos lembrar a fórmula que tinhamos lá em cima:
Então só falta calcular:
Que dá pra resolver pela substituição:
Bem mais tranquilo, que sorte... haha
Mas ai vamos ver como fica o em si:
Pronto, agora sim!