Determine e esboce a imagem da função vetorial
Passo 1
Nossa imagem é o vetor
Precisamos então achar uma relação entre as componentes desse vetor.
Como temos uma função vetorial de 2 variáveis, essa relação definirá uma superfície, que será a nossa imagem.
Passo 2
Observe que se chamarmos a terceira componente de , temos
E essa é a relação entre as três componentes da nossa função vetorial.
Passo 3
Maaas, ela ainda não nos diz muita coisa. Então, podemos mexer mais um pouquinho nela e vê onde chegamos.
OPA OPA! Isso ai já é alguma coisa!
E essa alguma coisa é um elipsoide, de centro na origem com focos em , em e em .
PORÉM! Repare que como na função vetorial original temos uma raiz quadrada em z, o elipsoide só vai pegar a parte positiva do eixo z.
Esboçando isso, temos:
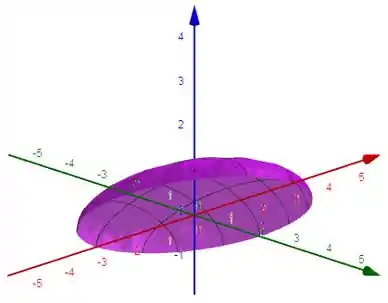
Resposta
A imagem de é o semi-elipsoide: