Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Ampère em Solenóides e Toróides

Ver Teoria
Exercício 2212345678910111213141516171819202123

Enunciado

Lei de Ampère, Materiais Magnéticos

A figura abaixo mostra uma bobina toroidal com N espiras bem compactadas. Uma corrente I percorre o enrolamento desta bobina.

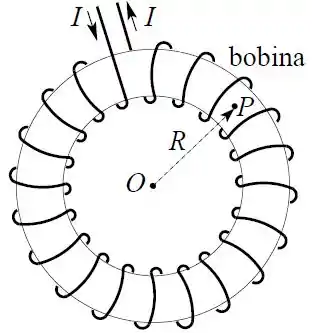
a ) Calcule o módulo do campo magnético B em um ponto P no interior da bobina, a uma distância R do seu eixo, quando a bobina é constituída só pelo enrolamento (núcleo de ar). Lembre que para o magnetismo o ar é praticamente indistinguível do vácuo.

b ) Calcule a relação entre as correntes I e I F e na bobina com núcleo de ar K m ≈ 1 e com núcleo de ferro K m ≈ 1400 , respectivamente que produzem o mesmo campo magnético B no ponto P .

c ) Calcule a suscetibilidade do alumínio se com o núcleo de alumínio e mesma corrente o campo magnético no ponto P passa a ser 1,00002 do valor no ar. Como se designa esse elemento segundo sua propriedade magnética?

Passo 1

a ) Calcule o módulo do campo magnético B em um ponto P no interior da bobina, a uma distância R do seu eixo, quando a bobina é constituída só pelo enrolamento (núcleo de ar). Lembre que para o magnetismo o ar é praticamente indistinguível do vácuo.

Pra calcular o campo magnético, vamos recorrer à Lei de Ampère, dada por:

∮ C   B → ∙ d l → = μ 0 I i n t

Dada a simetria do problema, a nossa curva será a circunferência de raio R por onde passa a bobina.

Além disso, como estamos falando que uma bobina de N espiras por onde passa uma corrente I , podemos dizer que I i n t = N I .

Então podemos simplificar a Lei de Ampère dessa forma:

B 2 π R = μ 0 N I

B = μ 0 N I 2 π R

Passo 2

b ) Calcule a relação entre as correntes I e I F e na bobina com núcleo de ar K m ≈ 1 e com núcleo de ferro K m ≈ 1400 , respectivamente que produzem o mesmo campo magnético B no ponto P .

Quando colocamos um material magnético, o campo magnético é multiplicado pelo valor de K m . Assim, o campo magnético para o ferro será:

B F e = K m μ 0 N I F e 2 π R

E para o ar, como K m ≈ 1 :

B a r = μ 0 N I 2 π R

O que queremos descobrir aqui é a relação entre I e I F e para que os campos magnéticos sejam iguais. Logo:

B F e = B a r

K m μ 0 N I F e 2 π R = μ 0 N I 2 π R

Simplificando esse cara de cima:

K m I F e = I

I I F e = K m ≈ 1400

Passo 3

c ) Calcule a suscetibilidade do alumínio se com o núcleo de alumínio e mesma corrente o campo magnético no ponto P passa a ser 1,00002 do valor no ar. Como se designa esse elemento segundo sua propriedade magnética?

Opa! Então agora o que o problema está dizendo é que:

B A l = 1,00002 B a r

Logo:

K m μ 0 N I 2 π R = 1,00002 μ 0 N I 2 π R

Simplificando esse cara:

K m = 1,00002

A relação entre K m e a suscetibilidade χ m é dada por:

K m = 1 + χ m

χ m = K m - 1

χ m = 1,00002 - 1

χ m = 0,00002

Logo, o alumínio é paramagnético.

Resposta

a )

B = μ 0 N I 2 π R

b )

I I F e ≈ 1400

c )

χ m = 0,00002

O alumínio é paramagnético.

Exercícios de Livros Relacionados

Uma casca cilíndrica longa, reta e de parede fina de raio R carrega uma corrente I paralela ao eixo central da casca. Encontre o campo magnético (incluindo a direção) dentro e fora da concha.
Um elétron é introduzido em uma das extremidades de um solenoide. Ao penetrar no campo magnético uniforme que existe no interior do solenoide, o eletron tem uma velocidade escalar de 800m / s e seu ve
Uma longa casca cilíndrica tem um raio interno ae um raio externo b e carrega uma corrente I paralela ao eixo central. Suponha que dentro do material da casca a densidade da corrente esteja uniformeme
Na Figura 27-55, uma corrente está 8,0 A na página, a outra corrente está 8,0 A fora da página e cada curva é um caminho circular. (a) Encontre ∫ B ⋅ d l para cada caminho, assumindo que cada integral
Uma lâmina fina e condutora no plano z=0 conduz corrente na direção -x (Figura 27-58a). A lâmina se estende indefinidamente em todas as dirigées e a corrente está uniformemente distribuída. Para deter