Considere a região do espaço
- Esboce hachurando
- Esboce hachurando
Passo 1
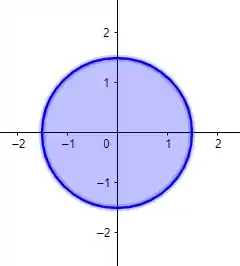
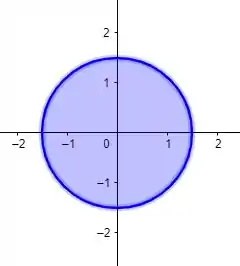
Bom, vamos primeiro entender qual é essa região aí de interseção da letra . Para isso, vamos substituir na equação de .
Isso nada mais é do que um disco. É como se fosse uma circunferência com centro na origem e raio , mas como tem o sinal de menor ou igual, incluiu o eu tá dentro dela tbm.
Além disso, é importante a gente ficar atento que esse disco tá na altura do plano .
Passo 2
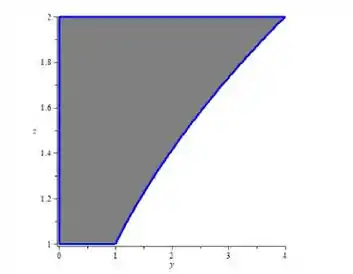
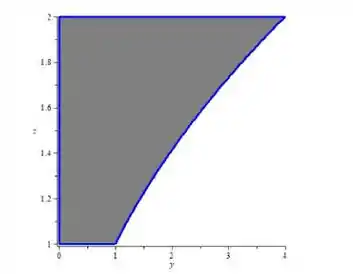
Agora vamos fazer na equação de .
E isso é uma parábola, ou melhor, o que está “fora” da parábola.
Lembrando que, do enunciado,
Assim, temos só uma parte da parábola.
Plotando isso no plano :
Resposta
Exercícios de Livros Relacionados
Calcule, caso exista.d) underset((x , y) - (0,0))(l i m) (x y)/(x^2 + y^2)
Calcule underset((h , k) - (0,0))(l i m) ((f (x + h , y + k) - f (x , y) - 2 x h - k))/(‖(h , k)‖) , onde f (x , y) = x^2 + y^2
1 - Calcule caso existae ) underset((x , y) - (0 , 0))(lim) (x y (x - y))/(x^4 + y^4)
Calcule, caso exista.b) underset((x , y) - (0,0))(l i m) (x)/(sqrt(x^2 + y^2))
Represente graficamente e o domínio da função z = f x , y dada por b) f x , y = 1 - z