Desenhar as curvas ou superfícies de nível dos seguintes campos escalares.
Passo 1
Eaew, belezinha?
A questão pede para a gente desenhar as curvas de nível da função f dada. Para calcular as curvas de nível dessa superfície, precisamos fazer uma de suas variáveis constante e analizar que tipo de função obtemos quando temos as duas variáveis restantes variando. Por exemplo, vamos começar fazendo
Fazendo isso, obtemos curvas nos planos paralelos ao plano z com equação
Ou seja, temos retas de y em função de x, quando olhamos a superfície pelo eixo z. A figura abaixo ilustra a situação para k = 1, 2 e 3.
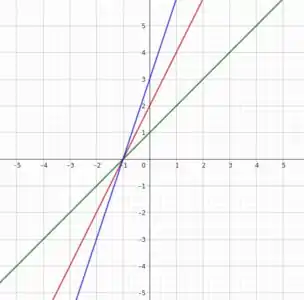
Agora vamos seguir o mesmo raciocínio para x constante e ver quais curvas obtemos. Então vamos lá!
Passo 2
Se fizermos x = k constante na função , obtemos
Como k é constante, temos que as curvas são também retas, mas que passam na origem. Para k= 0, 1, 2 temos as curvas ilustradas na imagem abaixo:
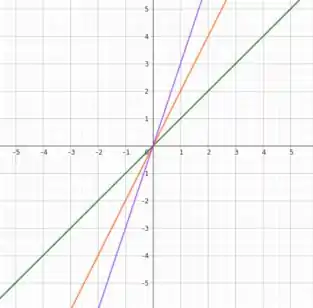
Agora só falta determinar o que ocorre quando fazemos y constante. Bora lá!
Passo 3
Da função , se fizermos y = k constante, obtemos curvas do tipo
Temos funções que caem conforme x aumenta. A figura abaixo ilustra as curvas de nível dessa situação:
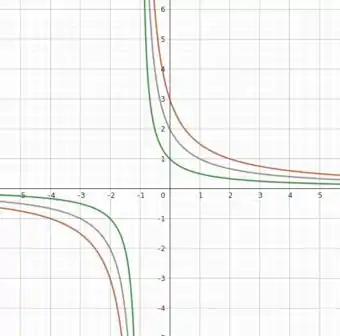
A figura a seguir ilustra a superfície definida por f(x,y):

Resposta
Desenvolvida ao longo da questão.