Resolva as questões abaixo:
- Considere a função . Determine os conjuntos de nível de e represente-os geometricamente no sistema de coordenadas adequado (reta, plano ou espaço tridimensional).
- Considere a função . Determine as curvas de nível de e represente-os geometricamente no sistema de coordenadas adequado (reta, plano ou espaço tridimensional).
- Considere a função . Determine as superfícies de nível de .
- Suponha que você chegue em uma sala de aula onde a única sentença escrita no quadro é “Faça um esboço do gráfico da função !”. Que desenho você faria?
Passo 1
Para representar os conjuntos de nível, fazemos:
Temos dois pontos na reta .
Ué, pontos?
Sim, pensa comigo: a função é uma curva no plano (que é uma parábola). Agora imagina que a gente corta essa parábola com retas paralelas pra formar os conjuntos de nível. O que temos como resultado quando uma reta corta uma curva são pontos.
Sacou?
Passo 2
Agora temos uma função de duas variáveis, mas com o irrestrito, de modo que temos um cilindro no qual o pode ter qualquer valor.
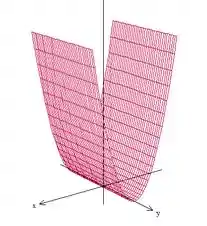
Se cortarmos o gráfico dessa função com planos ,
Temos as retas no plano.
Passo 3
Agora temos uma função de 3 variáveis em que e podem valer qualquer coisa.
Não conseguimos imaginar a cara que essa função tem, pois não sabemos desenhar no , mas sabemos que os conjuntos de nível dessa função de 3 variáveis estarão no espaço .
Assim, quando cortarmos nossa função com “coisas” paralelas iguais a em , teremos planos
No espaço .
Tá, eu sei que pareceu meio vudû isso, mas se você pensar comigo vai ver que faz sentido, olha só:
Quando tínhamos uma função de uma variável, os conjuntos de nível foram pontos (dimensão 0). Depois, quando passamos para uma função de duas variáveis, os conjuntos de nível passaram a ser retas (dimensão 1).
Ou seja, conforme aumentamos uma dimensão na função, aumentamos uma dimensão nos conjuntos de nível. Assim, quando temos uma função de três variáveis, os conjuntos de nível terão dimensão 2, ou seja, planos.
Sacou-se?!
Passo 4
Essa letra é meio WTF, né?!
Não sei você, mas eu faria o desenho de uma parábola, porque só tem uma variável aparecendo na função, então seria a primeira coisa que viria na minha cabeça.
Mas isso não quer dizer que eu (e você também) não saiba que mesmo que só uma variável esteja aparecendo, a função pode ter mais variáveis (as outras variáveis serão irrestritas, ou seja, poderão ter qualquer valor).
Resposta
- Dois pontos na reta
- Retas no plano
- Planos no espaço.