Na figura abaixo cinco fios paralelos longos no plano estão separados por uma distância .
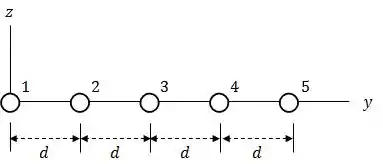
As correntes para dentro do papel são , , e , a corrente para fora do papel é Qual é o módulo da força por unidade de comprimento que age sobre o fio 3?
Passo 1
Beleza, o primeiro passo aqui é calcular o módulo de cada uma das forças em 3:
Passo 2
Beleza, o primeiro passo aqui é colocar graficamente onde estão cada uma dessas correntes para nos orientarmos... de acordo com o enunciado, o esquema é esse aqui:
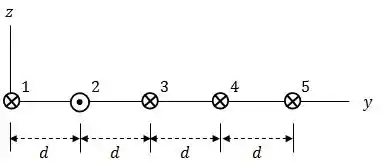
Lembrando que, quando as correntes são paralelas os fios se atraem e quando são antiparalelas, os fios se repelem.
Dessa forma:
Passo 3
A força resultante sobre o fio 3 será:
A força resultante por unidade de comprimento será:
Vou só dar uma arrumada pra facilitar os cálculos, de boa?
Onde:
Jogando esses valores na expressão acima, teremos: