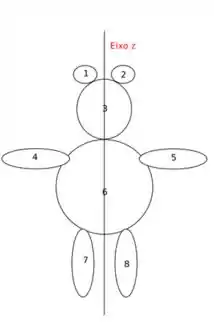
O momento de inércia, possui propriedades similares às do centro de massa, pois ambos são dados na forma de uma integral. Sendo assim, no cálculo do momento de inércia é possível dividir o domínio de integração em subdomínios e posteriormente somar o resultado. Por exemplo, para a figura abaixo (um urso”), basta calcular o momento de inércia de cada uma das sub-regiões numeradas de a em relação ao eixo , e depois somar o resultado:
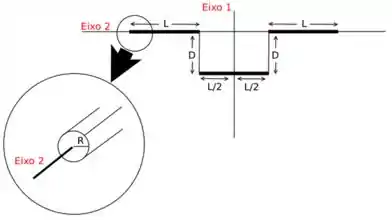
Sabendo disto, calcule o momento de inércia da figura abaixo em relação aos eixos e , supondo que as barras delgadas possuem massa desprezível e que as barras grossas possuem massa , são homogêneas e possuem secção reta circular de raio .
Dados: momento de inércia de um cilindro homogêneo de massa em relação ao eixo que passa pelo centro de sua secção reta de raio e pelo seu centro de massa: momento de inércia de uma barra homogênea de massa e comprimento em relação ao eixo que é perpendicular à extensão da barra e passa pelo seu centro de massa:
Passo 1
Fala aí galera, tudo bem?
Temos um enunciado GIGANTE aqui hein? Mas, vamos tentar resumir o que ele está falando.
Basicamente, temos a seguinte estrutura:
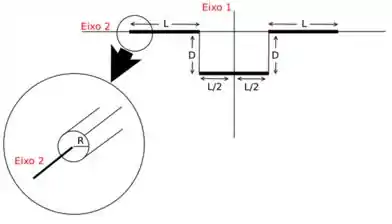
E, precisamos calcular o momento de inércia em relação ao eixo e ao eixo .
As barras grossas (as que aparecem escurinhas na imagem) são barras cilíndricas, com raio da secção circular valendo e massa . O enunciado ainda nos dá duas informações sobre o momento de inércia dessas barras:
O momento de inércia de uma dessas barras cilíndricas em relação a um eixo que passa pelo centro da secção reta circular vale:
O momento de inércia de uma dessas barras cilíndricas em relação a um eixo perpendicular à extensão da barra e que cruza o seu centro de massa vale:
Agora as coisas ficaram mais claras? Massa!
A nossa estratégia é calcular separadamente o momento de inércia de cada uma das barrinhas com relação ao eixo e depois com relação ao eixo . Pra fazer isso é bem importante utilizarmos o teorema dos eixos paralelos, que diz:
onde é a massa da estrutura que estamos calculando o momento de inércia e é a distância entre os eixos e . Beleza?
A ideia é essa, então vamo lá!
Passo 2
Vamos começar calculando o momento de inércia da estrutura com relação ao eixo . Para cada uma das barras, o momento de inércia com relação ao eixo perpendicular à sua extensão e que passa pelo seu centro de massa é dado por:
Beleza, isso já tínhamos visto no passo anterior.
Para calcular os seus momentos de inércia em relação ao eixo , precisamos usar o teorema dos eixos paralelos. Assim:
onde vai ser a distância entre o eixo perpendicular que passa pelo centro de massa da barra e o eixo . Analisando a figura:
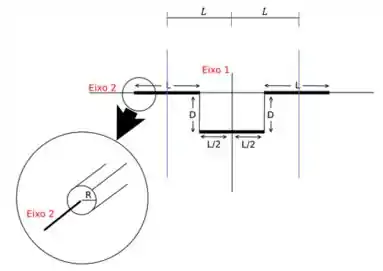
Temos que a distância para as duas barras superiores é de . Enquanto para a barra inferior, o eixo que perpendicular à sua extensão e que passa pelo seu centro de massa já coincide com o eixo .
Assim, temos:
Já para a barra inferior, vamos ter apenas:
Portanto, como temos duas barras superiores e uma barra inferior, sobre o momento de inércia de toda a estrutura com relação ao eixo podemos afirmar que:
Portanto:
Excelente!!! Já matamos a primeira parte 😊
Passo 3
Agora vamos calcular o momento de inércia da estrutura com relação ao eixo . Novamente o raciocínio é bem semelhante, como vimos no passo o momento de inércia de cada barrinha com relação ao eixo que passa pelo centro de sua secção reta circular vale:
Analisando a figura:
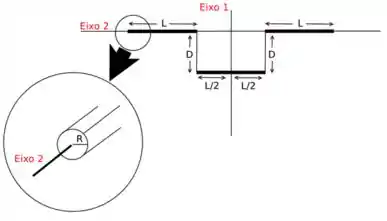
Vemos que para a barras superiores, esse eixo do centro da secção reta já coincide com o eixo . Mas, para a barra inferior os eixos estão há uma distância , assim:
Já para as barras superiores:
Logo, para a estrutura como um todo temos:
Logo:
Prontinho galera! Com isso matamos mais uma questão!
Espero que vocês tenham curtido a solução, até a próxima 😊