Empuxo(Princípio de Arquimedes)
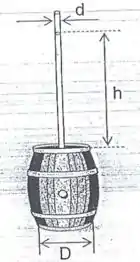
Quando apresentou o seu princípio, Pascal fez uma demonstração dramática. Ele inseriu um tubo fino de diâmetro verticalmente num barril fechado como mostra a figura abaixo. A tampa do barril tem um diâmetro Depois de preencher o barril com água, ele continuou preenchendo o tubo com água. Quando a altura da coluna de água no tubo atingiu a altura , o barril explodiu. Em um instante imediatamente anterior a explosão, calcule o que se pede.
Se necessário use , a densidade da água e
- O peso da água no tubo.
- A pressão manométrica da água logo abaixo da tampa do barril
- A força líquida(módulo, direção e sentido) na tampa do barril.
Passo 1
a):
Pra a gente achar o peso da água no tubo, basta a gente descobrir a massa de água presente ali. Pra isso, vamos usar a definição de densidade, ou seja:
O volume do tubo é a área de sua base vezes a altura:
Então a massa é:
E o peso:
Passo 2
b):
A pressão total abaixo da tampa do barril será igual a pressão da coluna de líquido do tubo mais a pressão da atmosfera(:
Mas a pressão manométrica é definida como a pressão total menos a pressão atmosférica, então:
Passo 3
c):
A força vai ser direcionada para cima e será vertical, pois é perpendicular a superfície do fluido. Além disso, a força vai ser dada pela pressão vezes a área:
Repare que aqui o que importa é a pressão exercida pela água! Então a pressão atmosférica não conta, por isso usamos a pressão manométrica.
Então:
Resposta
a)
b)
c)